Die Induktion einer elektrischen Spannung in einem Leiter aufgrund der Änderung des von dem Leiter selbst hervorgerufenen Magnetfelds.
Dieses Phänomen lässt sich besonders gut mit einer Spule untersuchen. In deren Inneren entsteht ein Magnetfeld, wenn ein Strom durch sie fließt. Ändert man den Strom, so ändert sich auch der magnetische Fluss \(\Phi\) durch den Spulenquerschnitt, was eine zusätzliche Spannung in der Schleife selbst induziert (daher der Name „Selbstinduktion“).
Die Selbstinduktion spielt bei Ein- und Ausschaltvorgängen eine wesentliche Rolle. Wenn z. B. in einem Gleichstromkreis mit Widerstand R eine einer Spannung U0 eingeschaltet wird, gilt nach dem Faraday’schen Induktionsgesetz für die induzierte Spannung Uind:
\(U_\text{ind} = - \dfrac{\text d \Phi}{\text d t} \equiv -\dot \Phi\)
Andererseits sind \(\Phi\) und die Stromstärke I im Kreis einander proportional mit dem Selbstinduktionskoeffizienten bzw. der Induktivität L als Proportionalitätskonstante: \(\Phi = L \cdot I\).
Durch Einsetzen und mit dem Ohm’schen Gesetz erhält man hieraus:
\(I = \dfrac{U_0 + U_\text{ind}} R = \dfrac 1 R \cdot \left( U_0 - L \dfrac{\text d I}{\text d t} \right) \quad \Leftrightarrow \quad L \dfrac{\text d I}{\text d t}+ R \cdot I = U_0\)
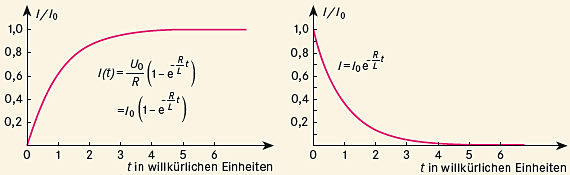
Lösungen dieser Differenzialgleichung sind in der Abbildung für den Einschalt- (links) und Ausschaltvorgang (rechts) skizziert. Man erkennt, dass sich die Endwerte \(I_0 = U_0/R\) bzw. 0 erst mit einer gewissen Verzögerung einstellen – auch im Gleichstromkreis fließt also nicht immer der gleiche Strom!
Wenn man zu dem hier diskutierten Kreis noch eine Kapazität (also einen Kondensator) hinzufügt, erhält man einen Schwingkreis.