Eine schiefe bzw. geneigte Ebene ist ein klassisches Untersuchungsobjekt der Mechanik, da sich hier Bewegungen je nach Neigungswinkel \(\alpha\) der Ebene so weit verlangsamen lassen, dass man auch ohne technische Hilfsmittel quantitativ erfassen kann – Galileo Galilei nutzt sie beispielsweise, als er seine Fallgesetze herleitete (die somit in gewisser Weise eher Rutsch- bzw. Rollgesetze waren). Außerdem ist die schiefe Ebene auch ein sog. einfache Maschine, da sich mit ihr Kraft einsparen lässt, indem man den Weg verlängert.
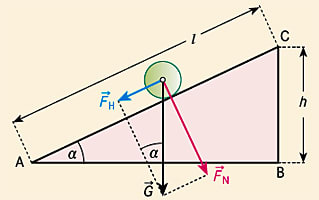
In der Abb. ist die Strecke AC die Länge l und die Strecke BC als Höhe h der schiefen Ebene. h und l hängen über die Beziehung \(h/l = \sin \alpha\) zusammen.
Am Schwerpunkt des eingezeichneten Körpers mit Masse m mit rundem Querschnitt greift dessen Gewichtskraft \(\vec G = m \cdot \vec g\) an, die man in eine hangabwärts gerichtete Komponente, die Hangabtriebskraft \(\vec F_\text H\), und eine dazu und zur Ebenenfläche senkrechte („normal stehende“) Normalkraft \(\vec F_\text N\) zerlegen kann. \(\vec g\) ist die Fallbeschleunigung.
Für die Beträge der Kräfte gilt:
\(F_\text H = G \cdot \sin \alpha = \dfrac {G \cdot h} l\)
bzw.
\(F_\text N = G \cdot \cos \alpha\)
Bewegt man den Körper mit der Gewichtskraft \(\vec G\) vom Beginn unten bis zum oberen Ende der Strecke l hinauf, so hat man eine Kraft vom Betrag FH entlang dieser Wegstrecke aufzubringen. Für die erforderliche Arbeit W gilt:
\(W = F_\text H \cdot l = G \cdot h\)
Das ist aber gerade die Hubarbeit, die erforderlich wäre, wenn man den Körper mit einer Kraft \(-\vec G\) (deren Betrag deutlich größer als FH wäre) senkrecht um den Weg h heben würde. Man kann also durch das Heben mit einer schiefen Ebene zwar Kraft sparen, aber keine Energie.
Es komplizierter wird die Behandlung der schiefen Ebene, wenn man Reibungseffekte berücksichtigt. Zum einen kann bei kleinem Neigungswinkel \(\alpha\) die Haftreibung so groß sein, dass es gar keine Bewegung gibt. Zum anderen muss man bei Gleitreibung die Vektorsumme der hangabwärtsgerichteten Kraft bilden, also den Ausdruck
\(\vec F_\text{ges} = \vec F_\text H - \vec F_\text{R, G} = \vec F_\text H - \mu_\text G \cdot \vec F_\text N\)
(\(\vec F_\text{R, G}\) ist die Gleitreibungskraft, \(\mu_\text G\) der Gleitreibungskoeffizient).
Übrigens: Die Bezeichnung „schiefe Ebene“ insofern irreführend, als man in der Regel nur eine eindimensionale hangabwärts gerichtete Bewegung betrachtet, eine „schiefe Strecke“ würde es also auch tun.