Der freie Fall ist ein auch historisch bedeutsamer Spezialfall der eindimensionalen, gleichmäßig beschleunigten Bewegung. Dabei bewegt sich ein Massenpunkt oder Körper nur unter dem Einfluss der von der Schwerenanziehung der Erde, also, wie der Name schon andeutet, nach unten. Der Luftwiderstand wird beim freien Fall vernachlässigt. Unter dieser Voraussetzung gilt die wichtige physikalische Aussage, dass alle Körper unabhängig von ihrer Masse gleich schnell fallen, die auch eine der Grundlagen der Allgemeinen Relativitätstheorie darstellt.
Für Präzisionsmessungen realisiert man den freien Fall entweder im Weltraum (etwa auf der Internationalen Raumstationen oder in Gravitationswellendetektoren auf Satellten) oder in evakuierten Fallröhren oder Falltürmen.
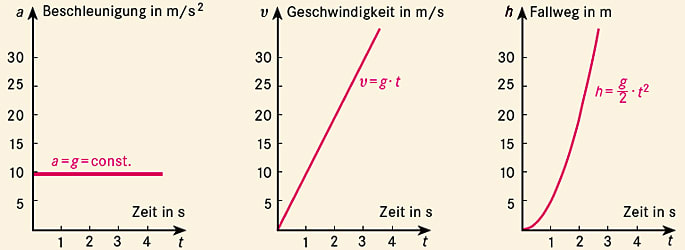
Die von Galileo Galilei Anfang des 17. Jh. gefunden Fallgesetze lauten:
- Die Fallgeschwindigkeit \(v\) wächst proportional mit der Fallzeit t, \(v = g \cdot t\), mit der Fallbeschleunigung g als Proportionalitätskonstante.
- Die Höhe h nimmt beim Fallen proportional zu t2 ab gemäß der Gleichung \(h = h_0 - \dfrac 1 2gt^2\)
Die erste Aussage folgt aus der zweiten, wenn man bedenkt, dass die Geschwindigkeit die zeitliche Ableitung des Wegs ist: \(\dfrac{\text d}{\text d t}\left( h_0 - \dfrac 1 2 gt^2 \right) = gt\).
Wie bei jeder gleichmäßig beschleunigten geradlinigen Bewegung sind das Geschwindigkeits-Zeit-Diagramm eine Gerade und das Weg-Zeit-Diagramm eine (halbe) Parabel (in der Abbildung ist die Ortskoordinate h wie üblich nach oben aufgetragen, natürlich erfolgt die Fallbewegung aber immer nach unten).