Das elektrische Feld legt an jedem Punkt des Raums Stärke und Richtung der Coulomb-Kraft \(\vec F_\text C\) fest, die dort auf eine punktförmige positive Probeladung Q wirkt. Die elektrische Feldstärke \(\vec E\) ist als Vektorgröße folgendermaßen definiert:
\(\vec E = \dfrac 1 Q \vec F_\text C\)
Im elektrischen Feld werden also die negativen Elektronen entgegen der Feldrichtung beschleunigt, positive Teilchen dagegen in Feldrichtung. Die SI-Einheit der elektrischen Feldstärke ist Newton pro Coulomb, wegen \(1\,\text{Nm} = 1\,\text{J} = 1\,\text V \cdot \text C\) gilt:
\(1\,\dfrac{\text N}{\text C} = 1\,\dfrac{\text{Nm} }{\text{Cm} } =1\,\dfrac{\text V}{\text m}\)
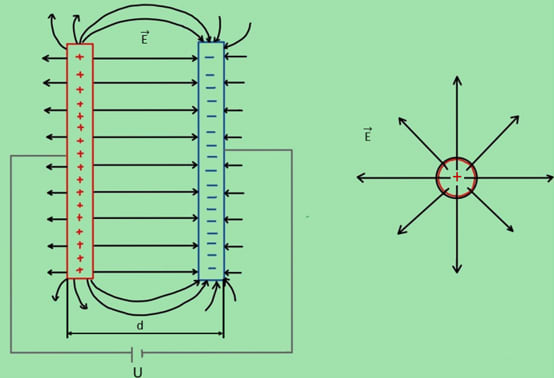
Die elektrischen Feldlinien beginnen und enden immer an elektrischen Ladungen. Man sagt daher auch, die elektrischen Ladungen seien die Quellen des Felds bzw. erzeugen das Feld.
Im Inneren eines Plattenkondensators ist das Feld annähernd homogen und für den Betrag gilt \(E = \dfrac U d\) (U: Spannung, d: Plattenabstand). Das Feld einer Punktladung ist kugelsymmetrisch, für den Betrag der Feldstärke gilt im Abstand r von der Punktladung \(E = \dfrac Q {4\pi\epsilon_0 r^2}\) (\(\epsilon_0\): elektrische Feldkonstante). Ganz allgemein gilt, dass das elektrische Feld die räumliche Ableitung des elektrischen Potenzials \(\varphi\) ist.
In Materie, wo es zu Polarisationseffekten kommen kann, wird manchmal auch der Vektor \(\vec D\) benutzt, den man die dielektrische Verschiebung nennt. Zwischen \(\vec E\) und \(\vec D\) gilt die Beziehung
\(\vec D = \epsilon \cdot \vec E = \epsilon_0 \epsilon_\text r \cdot \vec E\)
(\(\epsilon\): Dielektrizitätskonstante, \(\epsilon_0\): elektrische Feldkonstante, \(\epsilon_\text r\): Dielektrizitätszahl).
In der Elektrodynamik betrachtet man zeitlich variable elektrische Felder \(\vec E(\vec x,\, t)\). Dann verbinden sich elektrische und magnetische Erscheinungen und man spricht auch von den elektromagnetischen Feldern. Ein sich im Raum ausbreitende elektromagnetisches Feld ist eine elektromagnetische Welle.