-
Aufgabe 1
Dauer: 1 Minute 9 PunkteAnalysis, Teil 1
Aufgabe 1Die Bestimmung von Enzymaktivitäten in Serum, Plasma oder Harn hat in der medizinischen Diagnostik eine wichtige Bedeutung. Beispielsweise ist bei einem Herzinfarktpatienten die Serum-Enzymaktivität bestimmter Enzyme auch Tage nach dem Infarkt noch erhöht, sodass eine Spätdiagnose über die Messung der Enzymaktivität möglich ist.
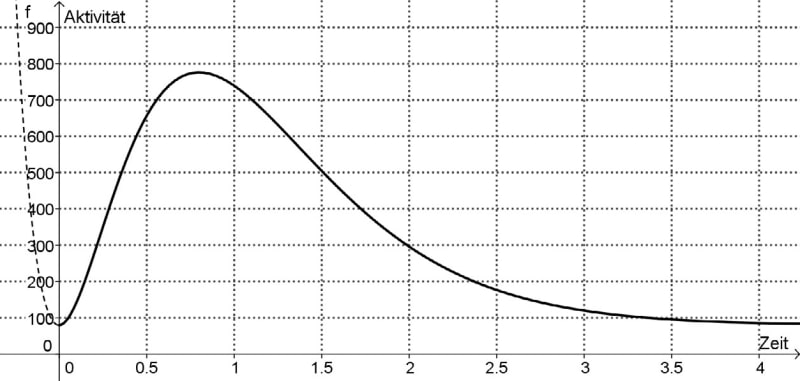
Der Verlauf einer bestimmten Enzymaktivitätskurve lässt sich durch den Graphen einer Exponentialfunktion der Schar \(f_{a,b,c}\) mit \(f_{a,b,c}(t)=a+b\cdot t^2\cdot e^{c\ \cdot\ t} \quad(a,b>0\ \text{und}\ c<0)\) approximieren (Material 1). Dabei steht \(t\) für die Zeit in Tagen seit Beginn einer Erkrankung und \(f(t)\) für die Enzymaktivität in Units (Substratumsatz pro Tag).
Bestimmen Sie die Parameter \(a\), \(b\) und \(c\) unter Berücksichtigung der folgenden Angaben:
- Die Enzymaktivität beträgt zu Beginn 80 Units.
- Bereits nach einem Tag ist die Enzymaktivität auf den Wert 740 Units gestiegen.
- Drei Tage nach Beginn hat sich die Enzymaktivität wieder weitgehend normalisiert und beträgt nur noch 120 Units.
(9 BE)
Material 1
-
Aufgabe 2
Dauer: 1 Minute 31 PunkteUm einen Herzinfarkt zu diagnostizieren, misst man beispielsweise die Aktivität des Enzyms Creatin-Kinase. Bei einem bestimmten Patienten kann die Aktivitätskurve für dieses Enzym für \(0\leq t \leq 5\) durch den Graphen der Exponentialfunktion \(f\) mit \(f(t)=100+4600\cdot t^2\cdot e^{-2\ \cdot\ t}\) angenähert werden, wobei \(t\) für die Zeit in Tagen nach dem Infarkt steht und \(f(t)\) für die Enzymaktivität in Units. Ca. 3 Tage nach einem Herzinfarkt befindet sich die Aktivität dieses Enzyms wieder im Normalbereich.
2.1
Zeigen Sie rechnerisch, dass gilt:
\(f''(t)=9200\cdot e^{-2 \cdot t}\cdot (2t^2-4t+1)\)
(6 BE)
2.2
Βerechnen Sie die Zeitpunkte, zu denen die Aktivitätskurve für das Enzym Creatin-Kinase am stärksten ansteigt bzw. am stärksten fällt, sowie jeweils die zugehörigen Änderungsraten.
Hinweis: Die Überprüfung der notwendigen Bedingung ist ausreichend.
(6 BE)
2.3
In Material 2 wird die Ermittlung einer Stammfunktion von \(f\) durch eine bestimmte Integrationsmethode angedeutet.
2.3.1
Geben Sie die Integrationsmethode an und leiten Sie durch Vervollständigung der Rechnung eine Stammfunktion \(F\) von \(f\) her.
(5 BE)
2.3.2
Bestimmen Sie das Integral \(\frac 1 3\cdot\int_0^3 f(t)\mathrm\ {d}t\) und deuten Sie das Ergebnis im Sachzusammenhang.
(4 BE)
2.4
Die Entscheidung für die Diagnose Herzinfarkt liege bei einer Enzymaktivität des Enzyms Creatin-Kinase von mindestens 192 Units. Zeigen Sie, dass der Ansatz \(100+4600\cdot t^2\cdot e^{-2\ \cdot\ t} = 192\) zu der Gleichung \(\mathrm{ln}\ \left(t^2\right)=2\cdot t - 3,91202\) führt. Diese Gleichung lässt sich nicht algebraisch lösen. Erläutern Sie die Darstellung in Material 3 und untersuchen Sie mithilfe der Graphen näherungsweise, in welcher Zeitspanne die Diagnose Herzinfarkt gestellt werden kann.
(10 BE)
Material 2
Material 3
-
Aufgabe 3
Dauer: 1 Minute 16 PunkteAnalysis, Teil 2
Aufgabe 1Im Material sind die Graphen einer Funktion der Funktionenschar \(f_k\) mit \(f_k(x) = \mathrm{sin}(x) + k·x,\ k \in \mathbb R\), und ihrer Ableitungsfunktion zu sehen.
1.1
Geben Sie die erste Ableitung von \(f_k \) an. Beschriften Sie die Graphen im Material jeweils mit der zugehörigen Funktion. Bestimmen Sie \(k\) für die im Material abgebildeten Funktionsgraphen.
(4 BE)
1.2
Untersuchen Sie unter Einbeziehung der Eigenschaften des Graphen der Ableitungsfunktion, für welche Werte von \(k\) die Scharfunktionen \(f_k \) Extremstellen haben.
(5 BE)
1.3
Skizzieren Sie im Material die Fläche zwischen dem Graphen von \(f_k \) und der Geraden mit der Gleichung \(y=k \cdot x\) über dem Intervall \([0;2π]\) für den in Aufgabe 1.1 bestimmten Wert von \(k\).
(2 BE)
1.4
Betrachtet werden für jede Scharfunktion \(f_k \) die Flächenstücke zwischen dem Graphen von \(f_k \) und der Geraden mit der Gleichung \(y=k \cdot x\), die jeweils von zwei aufeinanderfolgenden Schnittpunkten begrenzt werden. Zeigen Sie mithilfe geeigneter Rechnungen, dass alle diese Flächenstücke unabhängig von \(k\) gleich groß sind.
(5 BE)
Material
Graphen einer Funktion der Funktionenschar \(f_k\) mit \(f_k(x)=sin(x)+k\cdot x, \ k\in\mathbb R\) und ihrer Ableitungsfunktion.
-
Aufgabe 4
Dauer: 1 Minute 8 PunkteDer Temperaturverlauf eines Tages (gemessen in \(^°C\)) in Abhängigkeit von der Zeit \(t\) (gemessen in Stunden) kann modellhaft durch eine Funktion \(g\) dargestellt werden, die folgende Form hat:
\(g(t)=a\cdot \mathrm{sin}\left(\frac 1 {12}\pi\cdot(t-b)\right)+c,\ t\in \mathbb R,\ 0\leq t\leq24 \) und \(a,\ b,\ c\in \mathbb R\)
An einem bestimmten Tag wird um \(4\ \text {Uhr}\) morgens die tiefste Tagestemperatur von \(16\ ^°C\) gemessen. Im Laufe des Tages steigt die Temperatur auf einen Maximalwert von \(26\ ^°C\) an. Bestimmen Sie unter Nutzung Ihrer Kenntnisse über die Eigenschaften der Sinusfunktion zu den gegebenen Daten passende Werte für die Parameter \(a,\ b\) und \(c\). Beschreiben Sie die Bedeutung der Parameter im Sachzusammenhang.
(8 BE)
-
Aufgabe 5
Dauer: 1 Minute 16 PunkteAn einem bestimmten Tag wird in der Stadt Frankfurt am Main der Temperaturverlauf annähernd durch die Funktion \(h\) beschrieben mit:
\(h(t)=-6\cdot\mathrm{sin}\left(\frac \pi{12}t+\frac \pi{12}\right)+0,4t+10,5,\ t\in \mathbb R,\ 0\leq t\leq 24\)
(\(t\) in Stunden, \(h(t)\) in \(^°C\) auf eine Nachkommastelle genau angegeben.)3.1
Untersuchen Sie, zu welcher Uhrzeit die minimale und zu welcher Uhrzeit die maximale Temperatur erreicht wird.
Hinweis: Eine Betrachtung der Randwerte ist nicht erforderlich.
(9 BE)
3.2
Liegen nur wenige Temperaturmessungen vor, wird die mittlere Tagestemperatur näherungsweise nach der Formel \(T_L=\frac 1 4(T_0+T_6+T_{12}+T_{18})\) berechnet, wobei \(T_0,\ T_6,\ T_{12}\) und \(T_{18}\) die gemessenen Temperaturen zu den sogenannten „synoptischen Stunden“ um \(0,\ 6,\ 12\) und \(18\ \text{Uhr}\) des Tages bezeichnen. Berechnen Sie mithilfe von \(h\) und dieser Formel die mittlere Tagestemperatur an diesem Tag.
(3 BE)
3.3
Mit \(\overline T=\frac 1 {24}\int_0^{24}h(t)\ \mathrm d t\) kann ebenfalls eine sinnvolle mittlere Tagestemperatur berechnet werden. Berechnen Sie damit die mittlere Tagestemperatur in Frankfurt an diesem Tag. Berechnen Sie zudem die prozentuale Abweichung der Näherung durch die „synoptische Stunden“-Formel aus Aufgabe 3.2 vom hier berechneten Wert von \(\overline T\).
(4 BE)
-
Aufgabe 6
Dauer: 1 Minute 13 PunkteGeometrie, Teil 1
Aufgabe 1Das Dach eines quaderförmigen Gebäudes soll mit Solarkollektoren versehen werden (Material 1). Die in der x-z-Ebene gelegene Seitenfläche des Gebäudes weist dabei genau nach Süden.
Zur Vereinfachung der folgenden Berechnungen wird im Modell die Dachfläche des Gebäudes in die x-y-Ebene gelegt. Die Kollektorfläche der Solaranlage wird dann in dem in Material 1 vorgegebenen Koordinatensystem durch die Eckpunkte \(A(0,5|1|0),\ B(5,5|1|0),\ C(5,5|2,8|2,1)\) und \(D (0,5|2,8|2,1)\) beschrieben (alle Angaben in Metern).
1.1
Zeigen Sie rechnerisch, dass es sich bei dem Viereck \(ABCD\) um ein Rechteck handelt, und prüfen Sie, ob der für eine Kollektorfläche geforderte Mindestflächeninhalt von \(F = 13,5\ \text m^2\) unterschritten wird.
(4 BE)
1.2
Die Solaranlage arbeitet mit der größtmöglichen Leistung, wenn die Sonnenstrahlen senkrecht auf die Kollektorfläche treffen. Berechnen Sie die Richtung, in der die Sonnenstrahlen in diesem Fall auftreffen.
(4 BE)
1.3
Der Hersteller empfiehlt für die Kollektoren aus Gründen der Standfestigkeit, einen Neigungswinkel \(\alpha\) von \(50^°\) gegenüber der Dachfläche nicht zu überschreiten. Untersuchen Sie, ob dieses Kriterium für die geplante Anlage erfüllt ist.
(3 BE)
-
Aufgabe 7
Dauer: 1 Minute 9 PunkteTreffen die Sonnenstrahlen nicht orthogonal auf die Kollektorfläche, so ist die Leistung der Anlage reduziert. Dies wird berücksichtigt, indem man von einer reduzierten Kollektorfläche ausgeht, die als effektive Kollektorfläche \(F_{eff}\) bezeichnet wird. Die Leistung der Anlage ist proportional zum Flächeninhalt der effektiven Kollektorfläche. Material 2 zeigt die Lage der effektiven Fläche im Vergleich zur tatsächlichen Position der Kollektoren (Blickrichtung parallel zur x-Achse). Es ist ersichtlich, dass die Eckpunkte \(A \) und \(B\) ebenfalls Eckpunkte der effektiven Kollektorfläche sind.
2.1
Um die Effektivität der Solaranlage abzuschätzen, soll die Fläche \(F_{eff}\) für einen ungünstigen Sonnenstand berechnet werden, bei dem die Sonnenstrahlen durch den Vektor \(\vec v=\begin{pmatrix}0\\25\\-7\end{pmatrix}\) angegeben werden können. Berechnen Sie die Lage des im Material 2 eingezeichneten Punktes \( D'\). [zur Kontrolle: \(D'(0,5 \mid1,68 \mid 2,41)\)]
(7 BE)
2.2
Bestimmen Sie den Flächeninhalt der effektiven Kollektorfläche für den in Aufgabe 2.1 beschriebenen Fall und ermitteln Sie, wie viel Prozent der maximalen Leistung bei diesem Sonnenstand erzielt werden können.
(2 BE)
Material 1
Material 2
-
Aufgabe 8
Dauer: 1 Minute 10 PunkteUm zu überprüfen, ob weitere Kollektoren auf dem Dach aufgestellt werden können, ohne dass diese durch die bereits bestehenden Kollektoren beschattet werden, soll für den in Aufgabe 2.1 beschriebenen Sonnenstand der Schatten der Kollektorfläche \(ABCD\) auf der Dachfläche betrachtet werden.
3.1
Für beliebige Punkte \( P(x|y|z)\) können die Schattenpunkte auf der Dachfläche für den in Aufgabe 2.1 beschriebenen Sonnenstand durch eine Projektion in Richtung \(\vec v\) in die x-y-Ebene ermittelt werden. Bestimmen Sie die Matrix, die diese Projektion beschreibt.
(7 BE)
3.2
Berechnen Sie mithilfe Ihres Ergebnisses aus Aufgabe 3.1 die Schattenpunkte der Eckpunkte der Kollektorfläche auf der Dachfläche, und entscheiden Sie, ob der Schatten ganz auf der Dachfläche liegt. Falls Sie in Aufgabe 3.1 keine Lösung gefunden haben, verwenden Sie die Matrix:
\(M=\begin{pmatrix} 1&0&0\\ 0 &1&3,6\\ 0&0&0 \end{pmatrix}\)
(3 BE)
-
Aufgabe 9
Dauer: 1 Minute 17 PunkteGeometrie, Teil 2
Aufgabe 1Eine Fabrikhalle soll in einen gleichmäßig ansteigenden Hang hinein gebaut werden. Dazu wird aus dem Hang Erde abgetragen. Der entstehende Einschnitt in den Hang wird im Folgenden als Baugrube bezeichnet. Das Gelände vor der Baugrube ist eben und liegt in der x-y-Ebene. Der Übergang von der x-y-Ebene in den Hang wird von der Geraden \(g\) beschrieben, die durch die Punkte \(A(–10|30|0)\) und \(B(–30|90|0)\) verläuft (Material). Diese Punkte sind gleichzeitig die beiden vorderen Eckpunkte der rechteckigen Grundfläche der Baugrube. Der Punkt \(D(–40|20|0)\) ist ein weiterer Eckpunkt dieser Grundfläche.
Modellhaft kann angenommen werden, dass der Hang in einer Ebene \(H\) liegt. In dieser Ebene liegen auch die beiden oberen Eckpunkte \(E\) und \(F(–45|5|15)\) der Baugrube. Alle Angaben erfolgen in Metern.1.1
Berechnen Sie den fehlenden Eckpunkt \(C\) der Grundfläche \(ABCD\) der Baugrube. Bestätigen Sie durch Rechnung, dass diese Grundfläche bei \(A\) einen rechten Winkel besitzt.
(4 BE)
1.2
Geben Sie eine Gleichung der Hangebene \(H\) in Parameterform an und bestimmen Sie eine Koordinatengleichung dieser Ebene.
[zur Kontrolle: \(H: 9x + 3y + 26z = 0\)](6 BE)
1.3
Von einem festen Messpunkt \(P(30|20|5)\) außerhalb der Baustelle wird der obere Eckpunkt \(E\) der Baugrube über den Vektor \(\vec v=\begin{pmatrix}-21\\15\\2\end{pmatrix}\) anvisiert. Bestimmen Sie die Koordinaten des Punktes \(E\).
(4 BE)
1.4
Die Punkte \(D,\ C,\ E\) und \(F\) sind die Eckpunkte der „hinteren Wand“ der Baugrube. Sie liegen in der steil abfallenden Ebene \(J\). Eine Koordinatengleichung dieser Ebene lautet \(J: 3x + y + 2z = –100\). Nach Bauvorschrift darf eine solche Ebene gegenüber der Grundfläche höchstens einen Steigungswinkel von \(60^°\) besitzen.
Untersuchen Sie, ob die Ebene \(J\) die Vorgabe der Bauvorschrift erfüllt.
(3 BE)
-
Aufgabe 10
Dauer: 1 Minute 9 PunkteZwei Meter unterhalb des Mittelpunktes der Grundfläche \(ABCD\) beginnt die Entwässerungsleitung des gesamten Bauvorhabens. Sie hat ein gleichmäßiges Gefälle von \(2\ \%\). Die Gerade, die sich durch die Projektion der Entwässerungsleitung in die x-y-Ebene ergibt, hat den Richtungsvektor \(\vec v_{xy}=\begin{pmatrix}4\\3\end{pmatrix}\).
2.1
Bestimmen Sie für den dreidimensionalen Raum die Gleichung der Geraden \(g_E\), die den Verlauf der Entwässerungsleitung beschreibt.
[zur Kontrolle : \(g_E: \vec x=\begin{pmatrix}-35\\55\\-2\end{pmatrix}+s\begin{pmatrix}4\\3\\-0,1\end{pmatrix}\)](5 BE)
2.2
Der öffentliche Hauptkanal, an den die Entwässerungsleitung angeschlossen werden soll, lässt sich mithilfe folgender Geradengleichung modellhaft beschreiben:
\(g_E: \vec x=\begin{pmatrix}65\\20\\-3,5\end{pmatrix}+r\begin{pmatrix}-2\\4\\-0,01\end{pmatrix}\)
Da sich die Entwässerungsleitung und der Hauptkanal nicht schneiden, ist ein vertikaler, in Richtung der z-Achse verlaufender Fallschacht einzubauen, der die Entwässerungsleitung mit dem Hauptkanal verbindet. Ermitteln Sie die Höhe dieses Fallschachtes.
(4 BE)
Material
-
Aufgabe 11
Dauer: 1 Minute 4 PunkteEntwickeln Sie eine Lösungsstrategie, mit der das Volumen des Erdaushubs für die Baugrube berechnet werden kann. Erläutern die die einzelnen Schritte Ihres Lösungsweges. Eine Durchführung der entsprechenden Rechnungen ist nicht erforderlich.
(4 BE)
-
Aufgabe 12
Dauer: 1 Minute 10 PunkteStochastik
Aufgabe 1Im Folgenden werden mit „Internetnutzer“ alle privaten Internetnutzerinnen und Internetnutzer in Deutschland ab einem Alter von 10 Jahren bezeichnet.
28 % der Internetnutzer telefonieren über das Internet
Wiesbaden – \(28\ \%\) der Internetnutzer telefonierten im Jahr 2013 über das Internet. Dies teilte das
Statistische Bundesamt (Destatis) anlässlich des Weltkommunikationstages am 17. Mai 2014
mit.
Besonders beliebt ist diese Art der Kommunikation bei jungen Menschen: \(42\ \%\) der
Internetnutzer im Alter von 10 bis 24 Jahren nutzten 2013 dieses Medium zum Telefonieren. Bei
den 25- bis 54-Jährigen war es etwa jeder Vierte (\(26\ \%\)). Ältere Internetnutzer nahmen diese
technischen Möglichkeiten weniger in Anspruch: Bei den 55-Jährigen und Älteren telefonierte
etwa jeder Fünfte (\(21\ \%\)) über das Internet.
Im Jahr 2013 waren rund \(55\ \%\) aller Internetnutzer im Alter von 25 bis 54 Jahren.Daten entnommen aus: Statistisches Bundesamt, Zahl der Woche vom 13. Mai 2014
Im Jahr 2013 wird für eine weitere Untersuchung über das Nutzungsverhalten im Internet eine große Anzahl zufällig ausgewählter Internetnutzer befragt.
1.1
Bestimmen Sie die Wahrscheinlichkeit, dass unter den ersten zehn befragten Personen
- genau drei Personen dabei sind, die das Internet für Telefonate nutzen,
- höchstens drei Personen dabei sind, die das Internet für Telefonate nutzen.
(5 BE)
1.2
Von zehn der zufällig ausgewählten Internetnutzer weiß man, dass genau zwei das Internet für Telefonate nutzen. Die zehn Personen werden nacheinander in zufälliger Reihenfolge befragt. Bestimmen Sie die Wahrscheinlichkeit, dass unter den ersten drei Befragten genau einer dabei ist, der das Internet für Telefonate nutzt.
(5 BE) -
Aufgabe 13
Dauer: 1 Minute 7 PunkteDer Artikel über Internettelefonate in Deutschland enthält keine Angaben darüber, wie viel Prozent der Internetnutzer im Jahr 2013
- das Internet für Telefonate nutzen und im Alter von 25 bis 54 Jahren sind,
- 10 bis 24 Jahre alt sind.
Bestimmen Sie diese beiden Anteile.
(7 BE)
-
Aufgabe 14
Dauer: 1 Minute 13 PunkteSchon im Frühjahr 2014 ist man davon überzeugt, dass der Anteil der Internetnutzer, die das Internet zum Telefonieren nutzen, über \(28\ \%\) liegt und sich damit im Vergleich zu 2013 erhöht hat. Zur Überprüfung dieser Hypothese will man einen Test auf der Basis einer zufällig ausgewählten Stichprobe von 50 Internetnutzern durchführen.
3.1
Entwickeln Sie einen Hypothesentest mit einem Signifikanzniveau von \(1\ \%\) unter Angabe einer Entscheidungsregel.
(7 BE)
3.2
Angenommen, der Anteil \(p\) der Internetnutzer, die das Internet zum Telefonieren nutzen, hat sich im Frühjahr 2014 im Vergleich zu 2013 tatsächlich erhöht. Bei dem Funktionsgraphen im Material wird in Abhängigkeit von \(p_1\) die Wahrscheinlichkeit \(\beta\) dargestellt, bei einem zweiten Test zur Überprüfung derselben Hypothese mit dem Stichprobenumfang der Länge \( n = 50\) und einem im Vergleich zu Aufgabe 3.1 veränderten Signifikanzniveau \(\alpha\) einen Fehler 2. Art zu begehen (Operationscharakteristik). Geben Sie \(\beta\) bei diesem Test mithilfe des Materials an, wenn der tatsächliche Anteil \(p_1\) der Internetnutzer, die das Internet im Frühjahr 2014 zum Telefonieren nutzen, \(35\ \%\) beträgt, und erläutern Sie den Wert im Sachzusammenhang. Bestimmen Sie den zu diesem Test zugehörigen Ablehnungsbereich.
(6 BE)
Material
-
Aufgabe 1
Analysis, Teil 1
Aufgabe 1Die Bestimmung von Enzymaktivitäten in Serum, Plasma oder Harn hat in der medizinischen Diagnostik eine wichtige Bedeutung. Beispielsweise ist bei einem Herzinfarktpatienten die Serum-Enzymaktivität bestimmter Enzyme auch Tage nach dem Infarkt noch erhöht, sodass eine Spätdiagnose über die Messung der Enzymaktivität möglich ist.
Der Verlauf einer bestimmten Enzymaktivitätskurve lässt sich durch den Graphen einer Exponentialfunktion der Schar \(f_{a,b,c}\) mit \(f_{a,b,c}(t)=a+b\cdot t^2\cdot e^{c\ \cdot\ t} \quad(a,b>0\ \text{und}\ c<0)\) approximieren (Material 1). Dabei steht \(t\) für die Zeit in Tagen seit Beginn einer Erkrankung und \(f(t)\) für die Enzymaktivität in Units (Substratumsatz pro Tag).
Bestimmen Sie die Parameter \(a\), \(b\) und \(c\) unter Berücksichtigung der folgenden Angaben:
- Die Enzymaktivität beträgt zu Beginn 80 Units.
- Bereits nach einem Tag ist die Enzymaktivität auf den Wert 740 Units gestiegen.
- Drei Tage nach Beginn hat sich die Enzymaktivität wieder weitgehend normalisiert und beträgt nur noch 120 Units.
(9 BE)
Material 1