-
Aufgabe 1
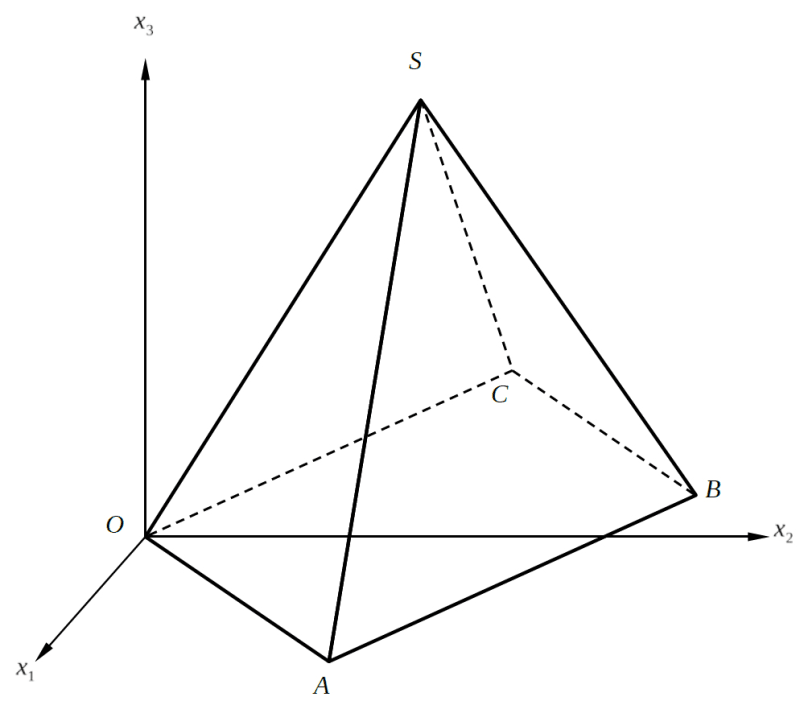
In einem kartesischen Koordinatensystem sind die Punkte \(O(0|0|0),\ A(9|12|0),\ B(-3|21|0),\ C(-12|9|0)\) und \(S(-1,5|10,5|15)\) Eckpunkte der Pyramide \(OABCS\), deren Grundfläche das Viereck \(OABC\) ist (siehe Abbildung).
Im Folgenden darf verwendet werden, dass die Seitendreiecke der Pyramide zueinander kongruent sind.
Abiturprüfung
Mathematik
Abitur