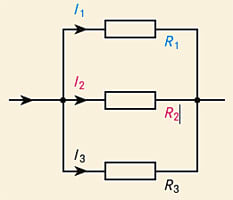
Bei einer Parallel- oder Nebeneinanderschaltung werden elektrische Leiterstränge bzw. Bauelemente (Widerstand, Kondensator usw.) so verschaltet, dass auf der einen Seite alle Eingänge der Bauelemente miteinander verbunden sind und auf der anderen Seite die Ausgänge (Abbildung). An allen n Bauelementen liegt die gleiche Spannung U an, der elektrische Strom I teilt sich dagegen auf in die Einzelströme I1, I1, ... , In (dies lässt sich aus den Kirchhoff’schen Regeln ableiten):
\(U = U_1 = U_2 = \ldots = U_n \\ I = I_1 + I_2 + \ldots + I_n\)
Für die Widerstände gilt, dass dehr Kehrwert des Gesamtwiderstands R (also der Leitwert G) der Summe der Einzelleitwerte bzw. der Summe der Kehrwerte der Einzelwiderstände entspricht:
\(\dfrac 1 R = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \ldots \dfrac{1}{R_n} \\ G = G_1 + G_2 + \ldots + G_n\)
Man kann sich dies herleiten, wenn man die Ströme in den einzelnen Leitersträngen als U/Ri schreibt. Beispielsweise beträgt für \(R_1 = 2 \Omega\) und \(R_2 = 3 \Omega\) der Gesamtwiderstand
\(\dfrac 1 R = \dfrac{1}{2\,\Omega} + \dfrac{1}{3\,\Omega} = \dfrac 5 6 \dfrac{1}{\Omega}\)
Generell ist bei Parallelschaltung der Gesamtwiderstand geringer als die Summe der Einzelwiderstände.
Die Kapazitäten von n parallelgeschalteten Kondensatoren addieren sich:
\(C = C_1 + C_2 + \ldots + C_n\)
Die Induktivitäten von n parallelgeschalteten Spulen verhalten sich wie die Widerstände:
\(\dfrac 1 L = \dfrac{1}{L_1} + \dfrac{1}{L_2} + \ldots \dfrac{1}{L_n}\)