Die Lorentz-Kraft (nach Hendrik. A. Lorentz) ist die Kraft, die eine elektrische Ladung Q seitlich ablenkt, wenn sie sich mit der Geschwindigkeit \(\vec v\) durch ein magnetisches Feld bewegt:
\(\vec F_\text L = Q \cdot \left[ \vec v \times \vec B \right] \equiv Q \cdot \vec v \times \vec B \)
(\(\vec B\): magnetische Flussdichte, „\(\times\)“ steht für das Vektor- bzw. Kreuzprodukt). Oft wird auch die elektrische Coulomb-Kraft auf die Ladung in die Gleichung miteinbezogen, dann gilt: \(\vec F_\text L = Q \cdot \left( \vec E + \vec v \times \vec B \right)\) mit \(\vec E\) als der elektrischen Feldstärke.
Ohne elektrisches Feld steht \(\vec F_\text L\) immer senkrecht auf \(\vec v\) und \(\vec B\). Für den Betrag FL der Lorentz-Kraft gilt dann:
\(F_\text L = Q \cdot v \cdot B \cdot \sin \alpha\)
wobei \(\alpha\) der von \(\vec v\) und \(\vec B\) eingeschlossene Winkel ist. Die Richtungen der drei beteiligten Vektoren kann man sich gut mit der Dreifingerregel veranschaulichen.
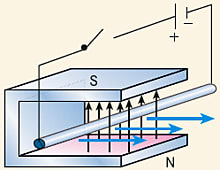
Ist der Stromkreis in der Abbildung geschlossen, so bewirkt die Lorentz-Kraft eine Abstoßung des Leiters in der gezeigten Richtung. Freie Ladungsträger bewegen sich im Magnetfeld \(\vec B\) auf kreisförmigen Bahnen. Den Radius r berechnet man, indem Lorentz- und Zentrifugalkraft gleichgesetzt werden:
\(Q \cdot v \cdot B \cdot \sin \alpha = \dfrac{m \cdot v^2} r\)
Wenn \(\vec v\) senkrecht auf \(\vec B\) steht (\(\alpha = 90°\)), so ergibt sich daraus
\(r = \dfrac{m \cdot v}{Q \cdot B}\)
Also kann man aus dem Bahnradius r die spezifische Ladung (das Verhältnis aus elektrischer Ladung und Masse, Q/m) eines Teilchens zu bestimmen.