Fadenpendel

Ein Fadenpendel ist ein Pendel, bei dem der möglichst schwere und kleine Pendelkörper an einem möglichst langen, dünnen und leichten Faden aufgehängt ist. Es ist ein bekanntes Beispiel für einen Oszillator, d. h. ein schwingfähiges System.

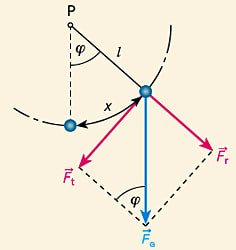
Besonders leicht zu behandeln ist die gedankliche Idealisierung des mathematischen Pendels: Bei diesem Pendel ist der Pendelkörper ein Massenpunkt m und der Faden der Länge l masselos und unendlich dünn (aber trotzdem beruhigend stabil!). Die Pendelmasse schwingt auf einem Kreisbogen vom Radius l periodisch um die Ruhelage. Als Auslenkung x bezeichnet man die Länge des Kreisabschnitts zwischen der Ruhelage und dem aktuellen Ort der Pendelmasse oder alternativ den Winkel \(\varphi\) zwischen Faden und Lot (Abb.).

Auf die Pendelmasse wirkt ihre Gewichtskraft \(\vec F_\text G\). Diese lässt sich in einen radialen Anteil \(\vec F_\text r\) und einen transversalen Anteil \(\vec F_\text t\) zerlegen. \(\vec F_\text r\) sorgt dafür, dass der Faden gespannt wird, \(\vec F_\text t\) dafür, dass der Massepunkt zurückgetrieben wird, ist also die Rückstellkraft, da diese Komponente immer der Bewegungsrichtung entgegengerichtet ist, also den Pendelkörper zur Ruhelage hin beschleunigt. Für den Betrag F_t gilt

\(F_\text t = F_\text G \cdot \sin \varphi\)

Da für kleine Winkel \( \sin \varphi \approx \varphi\) ist, ist der Betrag der Rückstellkraft für kleine Auslenkungen in guter Näherung proportional zum Auslenkungswinkel. Ersetzt man nun den Winkel \(\varphi\) im Bogenmaß durch das Verhältnis x/l und die Gewichtskraft F_G durch \(m \cdot g \cdot x\) (g: Fallbeschleunigung), ergibt sich:

\(F_\text t \approx \text G \cdot \varphi = G \cdot \dfrac x l = \dfrac {m \cdot g } l \cdot x\)

Die Rückstellkraft F_t ist also für kleine Ausschläge proportional zur Auslenkung x des Körpers aus der Ruhelage. Damit liegt ein lineares Kraftgesetz (wie beim Hooke’schen Gesetz) vor mit der Proportionalitätskonstanten \(D = \dfrac {m \cdot g } l \). Aufgrund dieses linearen Kraftgesetzes vollführt der Pendelkörper Sinusschwingungen. Für die Schwingungsdauer bzw. Periode des mathematischen Pendels ergibt sich dann:

\(T = 2\pi\cdot \sqrt {\dfrac l g }\)

Ein P. mit größerer Fadenlänge schwingt also langsamer. Die Schwingungsdauer hängt nicht von der Masse des Pendelkörpers ab, wohl ab er vom Planeten, auf dem man gerade steht (g ist nur auf der Erde annähernd konstant, auf dem Mars oder auch dem Mond dagegen deutlich kleiner).