Die Bragg-Gleichung (nach William Henry Bragg und seinem Sohn William Lawrence) gibt die Bedingung für das Zustandekommen von reflektierter Strahlung unter ganz bestimmten Winkeln bei der Beugung von Röntgen-, Elektronen- oder Neutronenstrahlen an einem Kristallgitter an. Die Bragg-Gleichung wird in der Kristallstrukturanalyse benutzt, um die Gitterkonstante des Kristalls zu bestimmen.
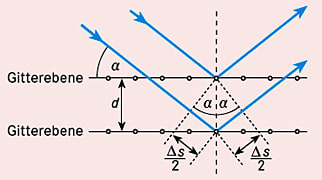
Die Argumentation ist im Prinzip die gleiche wie bei der Beugung von Licht an einem optischen Gitter, nur dass hier die in den Ebenen des Kristallgitters angeordneten Atome die Rolle der Gitterspalte übernehmen. Der Gangunterschied \(\Delta s\) zwischen zwei von benachbarten Gitterebenen reflektierten parallelen Strahlen mit Einfallswinkel \(\alpha\) beträgt (Abb.)
\(\Delta s = 2d\cdot \sin \alpha\)
Die reflektierten Strahlen interferieren konstruktiv, wenn \(\Delta s\) ein ganzzahliges Vielfaches der Wellenlänge \(\lambda\)l des Röntgenstrahls bzw. der Materiewelle beträgt, also \(\Delta s = k \cdot \lambda\) (k = 1, 2, 3, 4, ...). Nur für ganz bestimmte Winkel \(\alpha_k\) erhält man also ein messbares reflektiertes Strahlenbündel. Diese sog. Glanzwinkel müssen die folgende Bedingung erfüllen, welche die Bragg-Gleichung genannt wird:
\(k\cdot \lambda = 2d\cdot \sin \alpha_k\)k xl = 2 x d x sin ak .
Achtung: Der Glanzwinkel wird – anders als der Einfallwinkel bei Brechung oder Reflexion – nicht gegen das Einfallslot, sondern gegen die Gitterebene gemessen!