Was ist eine Kreisbewegung?
Kreisbewegung
Wie du mit der Formel für eine Kreisbewegung rechnest
Schritt-für-Schritt-Anleitung zum VideoZeige im FensterDrucken
Kreisbewegung berechnen
Was passiert mit einem Körper auf einer Kreisbahn?
Körper auf Kreisbahnen
Wie du mit der Formel für die Geschwindigkeit in einer Kurve rechnest
Schritt-für-Schritt-Anleitung
Aufgabe
Ein Auto mit einer Masse von einer Tonne fährt mit einer Geschwindigkeit von \(70 \frac{ \text{ km } }{\text{ h } }\) durch eine halbkreisförmige Kurve. Der Radius der Kurve beträgt \(60 \ \text{m}\).
- Beschreibe die Kräfte, die auf das Auto während der Kurve wirken. (Hinweis: Zentrifugalkraft, Zentripetalkraft)
- Gib die Größe der Zentrifugalkraft an.
Aufgabenteil a
Beschreibe die Kräfte, die auf das Auto während der Kurve wirken. (Hinweis: Zentrifugalkraft, Zentripetalkraft)
Schritt 1: Veranschauliche dir die Aufgabenstellung
Wenn du die Kräfte in einem System beschreiben möchtest, solltest du dir dieses immer als Erstes veranschaulichen. Eine gute Möglichkeit dazu ist, dir eine Skizze zu machen:
In der Skizze zeichnest du dir die gegebenen Informationen ein (Kurvenradius und Geschwindigkeit). Außerdem sind bereits die bei einer Kurvenfahrt stets wirkende Zentrifugalkraft und die ihr immer entgegengesetzt wirkende Zentripetalkraft angegeben.
Schritt 2: Schau dir die wirkenden Kräfte an
Die Zentripetalkraft ist die Kraft, die den Körper auf einer Kreisfahrt zum Mittelpunkt des Kreises zieht und so für das Einhalten der Kreisbahn sorgt. Die Zentrifugalkraft ist die Trägheitskraft, die der Zentripetalkraft entgegenwirkt.
Jetzt musst du dir überlegen, wie die Zentripetalkraft wirkt.
Schritt 3: Schau dir den spezifischen Versuch an
Du betrachtest ein Auto, das auf einer Straße fährt. Wie alle Körper wird auch das Auto durch die Schwerkraft auf der Erde gehalten. Diese wirkt allerdings nur nach unten und kann somit nicht als Zentripetalkraft zum Mittelpunkt der Kurve wirken. Trotzdem spielt sie eine indirekte Rolle, denn sie sorgt dafür, dass die Reifen auf die Straße gedrückt werden und damit einen Reibungswiderstand erzeugen. Wenn das Auto nun durch die Zentrifugalkraft nach außen gedrückt wird, müssten die Reifen auf der Straße eigentlich rutschen. Das Rutschen wird aber durch den Widerstand der Reibung verhindert. Und genau das ist unsere Zentripetalkraft: nämlich die Reibung zwischen Reifen und Straße.
Die wirkenden Kräfte sind also die Zentrifugalkraft, die durch die Kreisfahrt auf das Auto wirkt, und die Reibungskraft zwischen Reifen und Straße, die als Zentripetalkraft fungiert. Indirekt spielt außerdem die Schwerkraft eine Rolle, die das Auto auf die Straße drückt und so die Reibung erzeugt.
Aufgabenteil b
Gib die Größe der Zentrifugalkraft an.
Schritt 1: Finde, was gegeben und gesucht ist
Gegeben ist:
- die Masse des Autos: \(m = 1 \ \text{t}\)
- die Geschwindigkeit des Autos: \(v = 70 \ \frac{ \text{ km } }{\text{ h } }\)
- der Kreisradius der Kurve: \(r = 60 \ \text{m}\)
Und gesucht wird:
- die Größe der Zentrifugalkraft
Schritt 2: Finde die richtige Formel
Du möchtest wissen, wie groß die Zentrifugalkraft \(F_z\) ist. Daher liegt es natürlich nahe, die Formel für eben diese zu verwenden:
\(F_z = m \cdot \frac {v^2}r\)
Du kennst sowohl die die Masse \(m\) als auch die Geschwindigkeit \(v\) und den Kreisradius \(r\).
Schritt 3: Stell die Formel nach dem Gesuchten um
Da du die Zentrifugalkraft ausrechnen möchtest, musst du die Formel nicht weiter umstellen:
\(\color{red}{F_z} = m\cdot\frac{v^2}r\)
Für den Fall, dass du an anderer Stelle eine Formel umstellen musst, wird dir hier erklärt, wie es geht.
Schritt 4: Rechne die gegebenen Werte in die richtigen Einheiten um
Bevor du die Formel für die Zentrifugalkraft benutzen kannst, musst du die gegebenen Einheiten umrechnen.
Schau dir zunächst die Einheit der Zentrifugalkraft an. Sie wird in Newton N angegeben. Newton kann man aber auch wie folgt schreiben:
\([F]=1 \text {N}=1 \frac {\text {kg · m}} {s^2}\)
Deine Einheiten sollten also alle in den Einheiten Kilogramm, Meter und Sekunde angegeben sein.
Schau dir zunächst die Masse des Autos an. Sie ist in Tonnen angegeben. Du musst sie also in Kilogramm umrechnen. Die Umrechnungszahl ist 1000.
\(m = 1 \ \text{t}=1000 \ \text{kg}\)
Als Nächstes kannst du dir die Geschwindigkeit anschauen. Da hier die Einheiten km und h sind, musst du die Geschwindigkeit in Meter pro Sekunde umrechnen. Bei dieser Umrechnung musst du zwei Dinge gleichzeitig beachten:
Zum einen ist \(1 \ \text{km} = 1000 \ \text{m}\) und zum anderen \(1 \ \text{h} = 3600 \ \text{s}\).
\(v = 70 \ \text{km/h} = 70 \cdot\frac{1000}{3600} \ \text{m/s} \approx 19,4 \ \text{m/s}\)
Die Geschwindigkeit des Autos beträgt also: \(v = 19,4 \ \text{m/s}\).
Zum Schluss kannst du dir den Kreisradius anschauen:
\(r = 60 \ \text{m}\)
Dieser ist allerdings schon in Metern angegeben und muss nicht weiter umgerechnet werden.
Schritt 5: Setze die Werte in die Formel ein und rechne sie aus
Jetzt musst du noch deine Werte in die Formel für die Zentrifugalkraft einsetzen. Das Ganze sieht dann so aus:
\(F_z = m\cdot\frac{v^2}r = 1000\ \text{kg} \ \cdot\frac{(19,4 \frac{ \text{ m } }{\text{ s} })^2}{60 \ \text{m}}\)
Als Erstes solltest du das Quadrat ausrechnen, dann erhältst du:
\(F_z = 1000\cdot\frac{376,4}{60} \ \text{kg}\cdot\frac{\text{m}^{\not 2}}{\text{s}^2}\cdot\frac1{\not{\text m}} \approx 6273 \ \frac{\text{kg}\cdot\text m}{\text{s}^2}=6273 \ \text{N}\)
Damit man nicht immer so große Zahlen schreiben muss, werden Werte über 1000 N mit \(\text{kN}\) (Kilonewton) abgekürzt. Das kannst du vergleichen mit der Umrechnung von Meter auf Kilometer.
\(F_z \approx 6,2 \ \text{kN}\)
Auf das Auto wirkt also eine Zentrifugalkraft von ca. \(6,2 \ \text{kN}\).
Lösung
- Auf das Auto wirkt die Zentrifugalkraft aufgrund der Kreisfahrt und ihr entgegen wirkt die Reibungskraft als Zentripetalkraft. Zusätzlich wirkt die Schwerkraft, welche das Auto auf die Straße drückt und so die Reibung erzeugt.
- Das Auto erfährt eine Zentrifugalkraft von ca. \(6,2 \ \text{kN}\) bei der Fahrt durch die Kurve.
Kreisbahnen berechnen
Kreisbewegung
Was du wissen musst
-
Was ist das Besondere an einer Kreisbewegung?
Damit sich ein Körper auf einer kreisförmigen Bahn bewegt, muss sich die Richtung seiner Geschwindigkeit die ganze Zeit ändern. Würde das nicht passieren, dann würde sich der Körper einfach geradlinig nach vorn bewegen.
Das Besondere an der Kreisbewegung ist also die Beschleunigung. Sie ist immer vom Körper zum Drehzentrum gerichtet und die Ursache dafür, dass der Körper die Kreisbahn nicht verlässt. Durch ihre Wirkung wird die Richtung der Geschwindigkeit immer so verändert, dass sie zu jedem Zeitpunkt tangential zur Kreisbahn verläuft. Auch wenn der Betrag der Geschwindigkeit bei einer gleichförmigen Kreisbewegung gleich bleibt, handelt es sich also um eine beschleunigte Bewegung.
Weil der Geschwindigkeitsvektor nicht immer in die gleiche Richtung zeigt, handelt es sich um eine zweidimensionale Bewegung. Das ist ganz ähnlich wie beim waagerechten Wurf. Dort wird die Richtung der Geschwindigkeit ebenfalls geändert, denn die Gravitation zieht den geworfenen Körper nach unten. Dagegen ist der senkrechte Wurf eine eindimensionale Bewegung, denn hier bewegt sich der Körper immer nur auf einer geraden Linie (hoch und runter).
Besondere Größen der Kreisbewegung
Wie bei Übungen zur gleichmäßig beschleunigten Bewegung, geht es in der Physik bei Aufgaben und Übungen zur Kreisbewegung oft darum, die Beschleunigung zu berechnen, die auf den Körper wirkt und ihn damit auf der Kreisbahn hält.
Auch die Geschwindigkeit kommt beim Thema Kreisbewegung in vielen Aufgaben und Übungen vor. Hier musst du zwei Arten unterscheiden:
- Die Bahngeschwindigkeit entspricht bei der Kreisbewegung der normalen Geschwindigkeit, die du schon von der geradlinigen Bewegung kennst. Sie gibt an, welche Strecke der Körper auf seiner Kreisbahn pro Zeiteinheit zurücklegt, und wird wie üblich in der Einheit Meter pro Sekunde angegeben.
- Die Winkelgeschwindigkeit gibt dagegen an, welcher Winkel pro Zeiteinheit vom kreisenden Körper auf seiner Bahn überschritten wird. Sie wird in der Einheit eins durch Sekunden angegeben und ist eng mit der Umlaufzeit und der Frequenz einer Kreisbewegung verwandt.
Neben diesen Größen kommt auch die kinetische Energie oft in Aufgaben zur Kreisbewegung in der Physik vor.
-
Was ist der Unterschied zwischen Zentrifugalkraft und Zentripetalkraft?
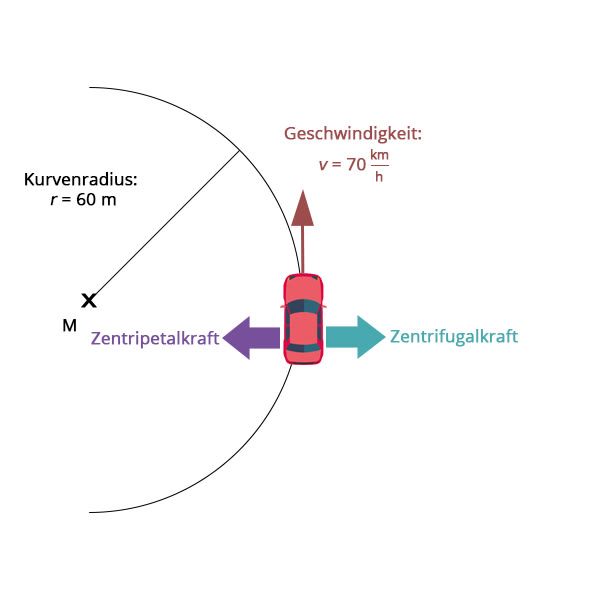
Na klar, zu der Beschleunigung, die vom Körper in die Richtung des Kreismittelpunkts wirkt und ihn damit auf seiner Kreisbahn hält, gehört eine Kraft. Das ist die Zentripetalkraft. Wie sie aufgebracht wird, hängt davon ab, wie die Kreisbewegung genau aussieht. In einem Kettenkarussell wird die Zentripetalkraft von den Ketten zur Verfügung gestellt. Wenn ein Satellit um die Erde kreist, dann wird die nötige Zentripetalkraft von der Gravitation aufgebracht. Oft spielt auch Reibung eine Rolle, wenn es darum geht, die Zentripetalkraft aufzubringen.
Die Zentrifugalkraft gibt es nur im beschleunigten Bezugssystem, also wenn du dich in dem Objekt befindest, das eine Kreisbewegung ausführt. Sie ist eine Trägheitskraft, die du vielleicht beim Autofahren schon einmal gespürt hast. Wenn das Auto in eine Kurve einfährt, dann widersetzt sich dein Körper zunächst der neuen Fahrtrichtung, denn er hat eine Masse und ist somit träge. Durch die Zentrifugalkraft wirst du etwas seitlich in deinen Sitz gepresst, und zwar in die Richtung, die aus der Kurve herauszeigt. Das ist die Zentrifugalkraft. In diesem Beispiel wird sie also durch Reibung (zwischen dir und deinem Sitz) aufgebracht. Sie ist genauso groß wie die Zentripetalkraft, zeigt aber in die entgegengesetzte Richtung, also nicht zum Mittelpunkt der Kreisbewegung, sondern nach außen.
-
Wozu braucht man Kreisbewegungen?
Die Kreisbewegung ist eine der fundamentalen Bewegungsarten und begegnet uns überall im Alltag, in der Natur und in technischen Anwendungen. Die Reifen deines Fahrrads oder Autos drehen sich ebenso im Kreis wie die Räder der Straßenbahn, und wenn wir mit diesen Fortbewegungsmitteln Kurven fahren, dann bewegen wir selbst uns auch auf einer Kreisbewegung. Helikopter und Turbinen von Flugzeugen benutzen Rotoren, die sich im Kreis drehen, um so Luft in eine bestimmte Richtung zu verdrängen und die Gegenkraft als Antrieb zu nutzen. Ebenso kommen Turbinen in vielen Arten von Kraftwerken vor und helfen dabei, Generatoren anzutreiben, die mechanische oder thermische Energie in elektrische Energie umwandeln. Auch die Rotoren von Windkraftanlagen werden durch die Kraft des Windes in eine Kreisbewegung versetzt.
Besonders wichtig für unser alltägliches Leben sind außerdem Satelliten, die um die Erde kreisen, uns unsere GPS-Daten zur Verfügung stellen und uns bei der Kommunikation mit unseren Handys behilflich sind. Auch die Erde selbst bewegt sich, wie die anderen Planeten unseres Sonnensystems, um die Sonne und führt dabei in guter Näherung eine Kreisbewegung aus.
