Zur Fehlerrechnung zählen verschiedene Verfahren zur rechnerischen Behandlung von Messfehlern in einer Messreihe.
Jede gemessene Größe a ist mit einem Fehler \(\Delta a\) behaftet, d. h., der wahre Wert der Größe liegt irgendwo im Intervall \(a \pm \Delta a\). Deshalb sollte man wann immer möglich beim Aufzeichnen von Messwerten in einem Diagramm (Koordinatensystem) an den Messpunkten Fehlerbalken einzeichnen. Auf diese Weise sieht man sofort, ob eine Abweichung zwischen gemessenem und theoretisch erwartetem Wert nur ein statistischer Mess- oder Ablesefehler ist oder ob man tatsächlich einen (möglicherweise nobelpreiswürdigen) neuen physikalischen Effekt beobachtet hat.
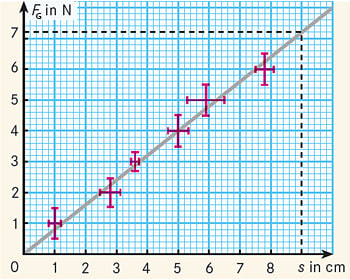
Viele mathematische Methoden der Fehlerrechnung sind recht kompliziert, deswegen benutzt man auch gerne grafische Verfahren. Beispielsweise wird bei einem vermuteten linearen Zusammenhang zwischen zwei Messgrößen (etwa die Gewichtskraft FG von Eisenstäben der Länge s) anstelle einer linearen Regression einfach eine Ausgleichsgerade gezeichnet, und zwar so, dass der Abstand zu den einzelnen Messpunkten so gering wie möglich ist (Abb.).