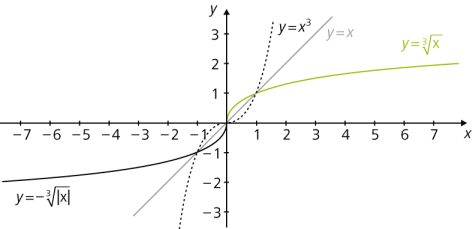
Die Umkehrfunktion f–1 einer Funktion f ordnet jedem Funktionswert f(x) der Funktion f den zugehörigen x-Wert zu:

\(f^{-1}\!: y \mapsto f^{-1}(y) = x\)  für jedes  y = f(x)

Dies ist dann und nur dann möglich, wenn die Funktion f eineindeutig bzw. bijektiv ist. „Eineindeutigkeit“ (Bijektivität) und „Umkehrbarkeit“ sind also äquivalente Eigenschaften.

Dies bedeutet insbesondere, dass jede Parallele zur x-Achse den Graphen einer umkehrbaren Funktion nur höchstens einmal schneidet (jeder Funktionswert kommt höchstens einmal vor).

Eine Funktion, die nicht auf ihrem gesamten Definitionsbereich umkehrbar ist, wird umkehrbar, wenn man sie auf einen monotonen Teilbereich einschränkt, z. B. hat die auf ganz \(\mathbb R\) nicht umkehrbare quadratische Funktion f(x) = x2 auf \(D_f'=\mathbb R_0^+\) die Umkehrfunktion \(f^{-1}(x) = \sqrt x\), also die (Quadrat-)Wurzelfunktion (siehe unten).

Es gelten die folgenden Aussagen:

  • Definitions- und Wertemenge von Funktion und Umkehrfunktion sind gerade vertauscht:
    \(D_f = W_{f^{-1}}; \ \ \ W_f = D_{f^{-1}}\)
  • Jede streng monotone Funktion ist umkehrbar. Ist f streng monoton steigend (fallend), gilt dies jeweils auch für f–1.
  • Die Hintereinanderausführung bzw. Verknüpfung von Funktion und Umkehrfunktion ergibt die identische Abbildung:
    \(f(f^{-1}(x)) = f^{-1}(f(x)) = x\)       bzw.   \((f \circ f^{-1})(x) = (f^{-1} \circ f)(x) = x\) 
    Anmerkung: Dies erklärt die Schreibweise „f–1“: Bei der Verknüpfung von Funktionen ist die Umkehrfunktion das inverse Element, also sozusagen der Kehrwert der Funktion f.
  • Die Funktionsgraphen von f und  f–1 gehen durch Spiegelung an der 1. Winkelhalbierenden, d. h. der Geraden y = x, ineinander über.

 

Funktionen und ihre Umkehrfunktionen

Funktion

\(D_f = W_{f^{-1}}\)

Umkehrfunktion

\(D_{f^{-1}} = W_f\)

Potenzfunktion f(x) = xn,
n gerade

\(\mathbb R_0^+\) (eingeschränkt)

Wurzelfunktion \(f^{-1}(x) = \sqrt[n]{x} = x^{1/n}\)

\(\mathbb R_0^+\)

Potenzfunktion f(x) = xn,
​n ungerade

\(\mathbb R\)

Wurzelfunktion \(f^{-1}(x) = \left\{ \begin{matrix} \sqrt[n]{|x|} = |x|^{1/n}\ (x \ge 0) \\ -\sqrt[n]{|x|} = -|x|^{1/n}\ (x < 0) \end{matrix} \right.\)

\(\mathbb R\)

Exponentialfunktionen f(x) = ax 
(\(a > 0, \ a \ne 1\))

\(\mathbb R\)

Logarithmusfunktionen \(\displaystyle f^{-1}(x) = \log_a x\)

\(\mathbb R^+\)

Winkelfunktionen f(x) = sin x, g(x) = cos x

\(\mathbb R\)

Arkusfunktionen \(f^{-1}(x) = \arcsin x \equiv \sin^{-1}x\),  \(g^{-1}(x) = \arccos x \equiv \cos^{-1}x\)

[1; –1]
 
So bestimmt man eine Umkehrfunktion
  1. Bereich ermitteln, in dem die Funktion umkehrbar ist.
  2. Funktionsgleichung y = f(x) nach x auflösen.
  3. „Variablentausch“: Bezeichnungen der Variablen y und x austauschen (Variablen sind willkürliche Benennungen und können im Prinzip jederzeit geändert werden).

Beispiel:
  \(f:x\mapsto y=0,5x+1, \ x \in \mathbb{R}\) 

  1. f ist in ganz \(\mathbb{R}\) streng monoton, also umkehrbar.
  2. \(y=0,5x+1 \ \ \Leftrightarrow \ \ 2 \cdot(y-1)=x \ \ \Leftrightarrow \ \ x=2y-2\)
  3. Tausch der Variablen: \(y=2x-2\)

Es ist also: \(f^{-1}:x\mapsto 2x-2, \ x \in D_{f^{-1}}=W_f= \mathbb{R}\)und \(W_{f^{-1}}=D_f=\mathbb{R}\). 

 

Schlagworte

  • #Funktionen