Eine Funktion, bei der die unabhängige Variable (das „x“) im Exponenten einer Potenz steht, heißt Exponentialfunktion. Die Basis ist dagegen eine Konstante bzw. ein Parameter, der nicht variiert wird. Formal definiert man eine Exponentialfunktion folgendermaßen:
\(f\!: x \mapsto f(x) = a^x\)
mit \(a \in \mathbb R^+ \setminus \{1\}\). Man schließt negative Basen aus, weil dies bei nicht ganzzahligem Exponent auf das Wurzelziehen aus einer negativen Zahl hinauslaufen würde, was verboten (genauer gesagt: mathematisch nicht definierbar) ist. Die Basen 0 und 1 würden zwar nicht zu undefinierten Ausdrücken führen, dafür aber zu höchst langweiligen: Für alle \(x \in \mathbb R\) ist 0x = 0 und 1x = 1.
Die Definitionsmenge der Exponentialfunktionen ist \(D_f = \mathbb R\), der Wertebereich ist \(W_f = \mathbb R^+\).
Man kann auch Exponentialfunktionen mit komplizierteren, von x abhängigen Termen im Exponenten oder mit additiven Konstanten usw. betrachten. In der Regel ist aber mit dem Ausdruck Exponentialfunktion das „Basismodel“ mit dem Funktionsterm ax gemeint.
Unter den Exponentialfunktionen spielt die mit der (irrationalen) Basis \(\text e \approx 2,718.281.828 \ldots\) eine ganz besondere Rolle in der Mathematik. Für diese sog. natürliche Exponentialfunktion, exp-Funktion oder noch kürzer e-Funktion gilt u. a., dass bei ihr Ableitung und Stammfunktion gleich der Funktion selbst sind: \(\left(\text e^x\right)' = \int \text e^x\text d x = \text e^x\). Die Zahl e nennt man die Euler’sche Zahl.
Beispiele:
-
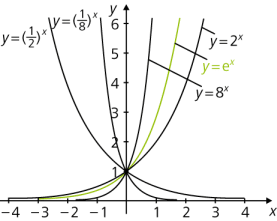
y = 2x, y = 8x, y = ex
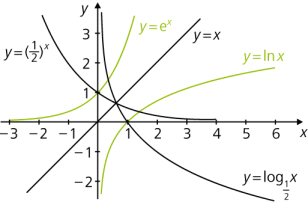
Die Umkehrfunktion der Exponentialfunktion ist die Logarithmusfunktion zur Basis a, logax, die der natürlichen Exponentialfunktion ist der natürliche Logarithmus ln x. Die Graphen liegen symmetrisch zur Geraden y = x, d. h., sie gehen durch Spiegelung an der 1. Winkelhalbierenden ineinander über.
Ersetzt man im Funktionsterm x durch –x, erhält man \(\displaystyle a^{-x}= \frac{1}{a^x} = \left( \frac 1 a \right)^x\). Dies bedeutet, dass der Funktionsgraph an der y-Achse gespiegelt wird, wenn die Basis durch ihren Kehrwert ersetzt wird. Man sieht weiterhin, dass für a > 1 der Funktionsgraph streng monoton steigt und für 0 < a < 1 streng monoton fällt.
Weitere Eigenschaften:
-
Exponentialfunktionen haben keine Nullstelle.
-
Gemeinsamer Punkt aller Exponentialkurven ist \((0|1)\).
-
Wegen ihrer Monotonie und wegen \(D_f = \mathbb R\) haben Exponentialfunktionen keine Extrema. Wegen \(\left(\text e^x\right)' = \text e^x\) gibt es auch keine Wendestellen.
-
Die x-Achse ist Asymptote der Exponentialkurven. Für 0 < a < 1 gilt \(\lim_{x \to \infty}a^x=0\) und für a > 1 ist \(\lim_{x \to -\infty}a^x=0\).
-
Wegen \(a^x = \left( \text e^{\ln a} \right)^x = \text e^{x \cdot \ln a}\) lässt sich jede Exponentialfunktion \(x \mapsto a^x\) auf die e-Funktion zurückführen.
Anwendung der Exponentialfunktionen:
Wachstumsprozesse (z. B. bei Bakterienkulturen) oder Abklingprozesse (z. B. beim radioaktiven Zerfall), bei denen die prozentuale Änderung in gleichen Zeiträumen (zumindest annähernd) konstant ist, können durch Exponentialfunktionen beschrieben bzw. modelliert werden.