Monotonie

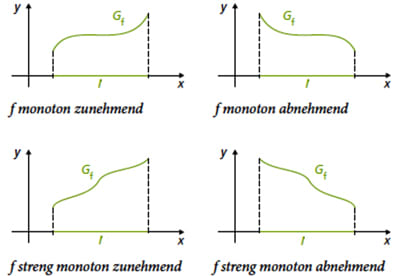
Eine Funktion \(f:\! x \mapsto g(x) \ \ (x\in D_f)\) heißt auf einem Intervall \(I \subset D_f\) genau dann

• monoton steigend (zunehmend), wenn für alle \(x_1, x_2 \in I\) gilt: \(x_1< x_2 \ \ \Rightarrow \ \ f(x_1) \le f(x_2)\)
• streng monoton steigend (zunehmend), wenn für alle \(x_1, x_2 \in I\) gilt: \(x_1< x_2 \ \ \Rightarrow \ \ f(x_1) < f(x_2)\)
• monoton fallend (abnehmend), wenn für alle \(x_1, x_2 \in I\) gilt: \(x_1< x_2 \ \ \Rightarrow \ \ f(x_1) \ge f(x_2)\)
• streng monoton fallend (abnehmend), wenn für alle \(x_1, x_2 \in I\) gilt: \(x_1< x_2 \ \ \Rightarrow \ \ f(x_1) > f(x_2)\)

Beispiel:
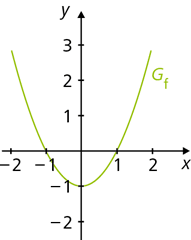
\(f:x \mapsto x^2-1, \ x \in \mathbb{R}\)
Sind \(x_1,x_2 \in \mathbb{R}\) mit \(x_1<x_2\), so ist \(f(x_2)-f(x_1)=(x_2^2-1)-(x_1^2-1)=x_2^2-x_1^2\).
Es gilt nun für \(x_1<x_2\leq0\): \(f(x_2)-f(x_1)=x_2^2-x_1^2<0\) und für \(0\leq x_1<x_2\): \(f(x_2)-f(x_1)=x_2^2-x_1^2>0\).

f ist also streng monoton fallend im Intervall \(]-\infty ; 0]\) und steigt streng monoton im Intervall \([0;+\infty[\).

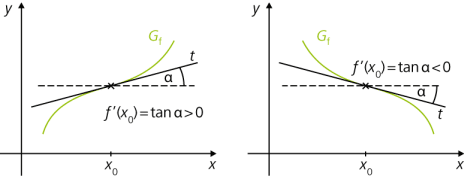
Wenn der Graph G_f einer differenzierbaren Funktion f streng monoton steigt, ist seine erste Ableitung positiv (\(f'(x) > 0\)), steigt er „nur“ monoton, gilt \(f'(x)\ge 0\).

Wenn er streng monoton fällt, ist seine erste Ableitung negativ (\(f'(x) < 0\)), fällt er „nur“ monoton, gilt \(f'(x) \le 0\).

Anmerkung: Der Graph G_f besitzt an einer Stelle x₀ genau dann eine waagrechte Tangente, wenn \(f' (x) = 0\).