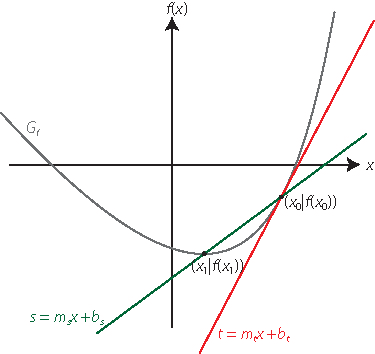
In der Differenzialrechnung gibt die Ableitung einer Funktion f an einer Stelle x0 an, wie steil die Tangente an die Funktion in diesem Punkt verläuft, genauer gesagt deren Steigung mt. Dies ist genau dann möglich, wenn die Funktion f an dieser Stelle differenzierbar ist. Ist sie in einem Intervall bzw. im gesamten Definitionsbereich differenzierbar, dann ist die Ableitung der Funktion f dort selbst eine Funktion, die man \(f'\) („f Strich“) nennt, besonders in der Physik auch \(f'(x) \equiv \dfrac {\text d f}{\text d x} = \dfrac {\text d}{\text d x}f(x)\) („d f nach d x“).
Die Ableitung wird formal definiert als der Grenzwert des Differenzenquotienten bei Annäherung an x0:
\(\displaystyle f'(x_0)= \lim_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}\) bzw. \(\displaystyle f'(x_0) = m_t= \lim_{x \to x_0} m_s\)
mit der Sekantensteigung ms. Man nennt die Sekantensteigung auch Differenzenquotient und ihren Grenzwert, die Tangentensteigung, den Differenzialquotienten an der jeweiligen Stelle.
Man kann die Ableitung einer Funktion auch als ihre momentane Änderungsrate interpretieren.
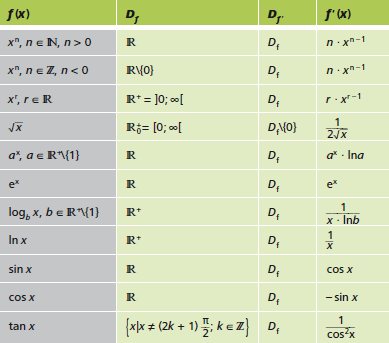
Für das Ableiten (Differenzieren) gelten die Ableitungsregeln, die man sich unbedingt einprägen sollte. Die folgende Tabelle zeigt die Ableitungen wichtiger Grundfunktionen:
Höhere Ableitungen
Wenn die Ableitungsfunktion \(f'\) ebenfalls differenzierbar ist, so nennt man die Ableitungsfunktion von \(f'\) die zweite Ableitung von \(f\). Sie wird mit \(f''\) (lies: „\(f\) zwei Strich“) bezeichnet.
Schreibweisen:
\(f'': x \mapsto f''(x) \ \ (x \in D_{f''})\) bzw. \(\displaystyle f''(x) =\frac{d^2f(x)}{dx^2}=\frac{d^2}{dx^2}f(x)\) (lies: „d zwei f von x nach dx Quadrat“)
Genauso werden die dritte, vierte, ... n-te Ableitung einer Funktion definiert. Sie wird mit \(f''', f^{(4)} , f^{(5)} , ... f^{(n)}\) bezeichnet.
Wenn die n-te Ableitung einer Funktion existiert, heißt die Funktion n-mal differenzierbar.