Eine Ellipse ist eine geometrische Figur, die man als einen verallgemeinerten (einfacher gesagt: mehr oder weniger platt gedrückten) Kreis auffassen kann. Wie der Kreis ist die Ellipse ein Kegelschnitt, also eine mögliche Planeten- oder Kometenbahn (die Erdbahn ist beispielsweise eine Ellipse, deswegen ist der Erde der Sonne im Januar etwas näher als im Juli).
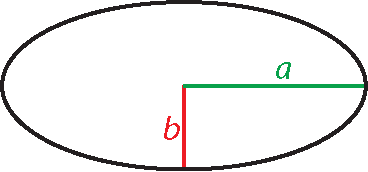
Den längsten bzw. kürzesten Abstand zwischen Mittelpunkt und Umfang der Ellipse nennt man große und kleine Halbachse der Ellipse, a und b. Bei einem Kreis sind die beiden Halbachsen gleich lang und entsprechen dem Radius, also a = b = r. Die Ellipse ist außerdem das Schrägbild des Kreises bzw. der kreisförmigen Grundfläche eines Körpers (z. B. bei Kegel oder Zylinder).
Für Punkte auf dem Umfang einer Ellipse mit Mittelpunkt im Ursprung und großer Halbachse auf der x-Achse gilt die Gleichung
\(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1\)
Für a = b = r geht dies in die Kreisgleichung x2 + y2 = r2 über.