Der Begriff Zuordnung (Relation) wird in der Mathematik und speziell in der Schule nicht ganz einheitlich gebraucht. Manchmal ist damit einfach ein anderes Wort für Funktion gemeint (siehe unten), meist aber geht es eine ganz allgemeine Abbildung zwischen den Elementen zweier Mengen X und Y. In der Regel hat man es dabei mit Zahlenmengen zu tun.
Man kann drei Fälle unterscheiden:
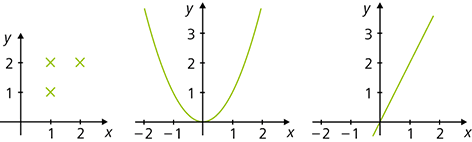
- Mehrdeutige Zuordnung: Jedem Element x aus der Urbildmenge oder Ausgangsmenge X können beliebig viele Elemente der Bildmenge oder Zielmenge Y zugeordnet werden (in der Abbildung links).
- Eindeutige Zuordnung: Jedem Element x aus der Urbildmenge oder Ausgangsmenge X wird höchstens ein Element y der Bildmenge oder Zielmenge Y zugeordnet, es können aber mehrere Elemente aus X zum selben y gehören (mittlere Abbildung).
Eine eindeutige Zurordnung ist eine Funktion. - Eineindeutige Zuordnung: Jedem Element x aus der Urbildmenge oder Ausgangsmenge X wird genau ein Element y der Bildmenge oder Zielmenge Y zugeordnet – und umgekehrt (in der Abbildung rechts).
Eine eineindeutige Zuordnung besitzt eine Umkehrfunktion.
Man kann eine Zuordnung durch eine Wertetabelle, einen Pfeilgraph, als Paarmenge oder als Graph im Koordinatensystem (Achsenkreuz) darstellen.
Im Koordinatensystem wird die Ausgangsmenge X i. A. auf der horizontalen Achse und die Zielmenge Y auf der vertikalen Achse angetragen. Zum Graphen der Zuordnung gehören alle Punkte, deren Koordinaten (x|y) die Zuordnung erfüllen.