Eine Menge ist, ganz allgemein formuliert, entweder etwas, das andere Objekte (Dinge, Wesen oder was auch immer) enthält, die man die Elemente der Menge nennt. Der Begriff der Menge ist so abstrakt wie grundlegend für die Mathematik, es gelten nur die folgenden Bedingungen:
- Man kann von jedem Objekt sagen, ob es Element einer bestimmten Menge ist oder nicht.
- Ein Element kann auch mehrfach bzw. beliebig oft in einer Menge enthalten sein.
- Es gibt in einer Menge keine Reihenfolge oder sonstige Ordnung, wichtig ist nur „drin oder nicht“.
- Mengen können kein Element, endlich viele Elemente oder unendlich viele Elemente enthalten.
- Es gibt nur eine Menge, die kein Element enthält, diese heißt leere Menge und wird mit den Zeichen „{}“ oder „\(\emptyset\)“ symbolisiert.
In der Mathematik hat man meistens (aber nicht immer!) mit Zahlenmengen zu tun, also mit Mengen, deren Elemente Zahlen sind. Unter diesen spielen wiederum die sog. Zahlenbereiche eine besondere Rolle, also die Mengen \(\mathbb N\), \(\mathbb Z\), \(\mathbb B\), \(\mathbb Q\) und \(\mathbb R\).
Mengen werden gewöhnlich mit Großbuchstaben symbolisiert. Man kann sie entweder angeben, indem man, soweit möglich, alle Elemente in beliebiger Abfolge zwischen geschweiften Klammern auflistet, oder indem man eine Bedingung angibt, welche eindeutig festlegt, ob etwas in der Menge ist oder nicht.
Beispiele:
- Menge der einstelligen Primzahlen: A = {2; 3; 5; 7}
- Menge der ganzen Zahlen: \(\mathbb Z = \{\ldots; -3; -2; -1; 0; 1; 2; 3; \ldots \}\)
- Lösungsmenge der quadratischen Gleichung x2 = 4: L = {–2; 2} = {x| x2 = 4} (sprich: „L ist die Menge aller x, für die gilt: x2 = 4“)
- Menge der geraden natürlichen Zahlen: \(A = \{n| n\in \mathbb N\ \land\ n : 2\in \mathbb N\}\)
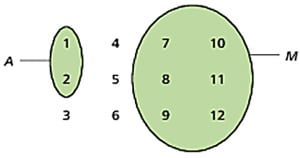
Außerdem ist es bei Mengen mit endlich vielen Elementen möglich, grafisch anzugeben, ob ein Element zu einer Menge gehört oder nicht (Mengenbild):
Die Mengen A und M aus der Grafik werden in aufzählender Form so geschrieben: A = {1; 2}, M = {7; 8; 9; 10; 11; 12}.
Wenn 8 in M enthalten ist, schreibt man: „\(8\in M\)“ (sprich: „8 ist Element von M“), wenn 4 nicht in M liegt, schreibt man „\(4\notin M\)“4 ∉ M (sprich: „4 ist kein Element von M“).
Man kann in gewisser Weise auch mit Mengen rechnen:
- Die Vereinigungsmenge \(A \cup B\) (sprich: „A vereinigt B“) zweier Mengen A und B enthält alle Elemente von A und B beziehungsweise alle Elemente, die in A, in B oder in beiden Mengen enthalten sind.
- Die Schnittmenge \(A \cap B\) (sprich: „A geschnitten B“) zweier Mengen A und B enthält alle Elemente, die sowohl in A als auch in B enthalten sind.
- Die Restmenge \(A \setminus B\) (sprich: „A ohne B“) zweier Mengen A und B enthält alle Elemente, die in A, aber nicht in B enthalten sind.
- Wenn alle Elemente von A in B enthalten sind, nennt man A eine Teilmenge von B und schreibt \(A \subset B\) (sprich: „A enthalten in B“).
- Die Menge aller Teilmengen einer Menge M ist ihre Potenzmenge \(\mathcal{P}(M)\).
Weitere häufig auftretenden Mengen sind Grundmenge, Definitionsmenge und Wertemenge von Gleichungen und Funktionen, die Lösungsmenge einer Gleichung oder eines Gleichungssystems, Ergebnismenge eines Zufallsexperiments sowie die Teilermenge einer natürlichen Zahl.