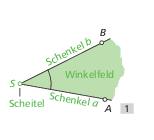
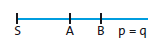Zwei Strahlen mit einem gemeinsamen Anfangspunkt S bilden einen Winkel. Der gemeinsame Anfangspunkt ist der Scheitelpunkt des Winkels. Die zwei Strahlen nennt man die Schenkel des Winkels. Meistens gibt man Winkel mit kleinen griechischen Buchstaben an, z. B. \(\alpha\) (alpha), \(\beta\) (beta), \(\gamma\) (gamma), \(\delta\) (delta) oder \(\varphi\) (phi).
Einen Winkel der Größe 1 Grad (1°) erhält man, indem man einen Kreis in 360 deckungsgleiche Teile (Kreisausschnitte) zerlegt. Außer im Gradmaß werden Winkel oft auch im Bogenmaß angegeben.
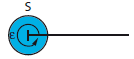
Wird der eine Schenkel um den Scheitelpunkt S im Uhrzeigersinn zum anderen Schenkel gedreht (in der Abbildung also der untere Schenkel zum oberen hin), so spricht man von einem orientierten Winkel, und das Winkelmaß hat einen positiven Wert. Im umgekehrten Fall ist der Winkel negativ (orientiert).
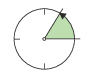
Je nach Größe des Winkels gibt es besondere Namen für die sog. Winkelarten, wie sie in den folgenden Skizzen auftreten:
 |
 |
|
|
|
|
spitzer Winkel \(\alpha\): \(\alpha\) < 90˚
|
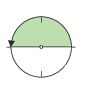
gestreckter Winkel \(\delta\): \(\delta\) = 180˚
|
überstumpfer Winkel \(\mu\): 180˚ < \(\mu\) < 360˚
|
Vollwinkel \(\epsilon\): \(\epsilon\) = 360˚ |
Nullwinkel \(\alpha\): \(\alpha\) = 0˚ |
Für die an einer Geradenkreuzung bzw. an geschnittenen Parallelen auftretenden Winkel gelten besondere Sätze (Scheitelwinkelsatz, Nebenwinkelsatz usw.).
Winkel treten insbesondere an geometrischen Figuren und Körpern auf wie Dreieck, Viereck, Polygon (Vieleck) oder Würfel.
In der Analytischen Geometrie kann man Winkel zwischen Geraden und/oder Ebenen mithilfe von Vektoren berechnen.