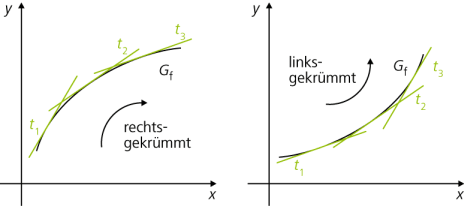
Das Krümmungsverhalten von Funktionsgraphen lässt sich anschaulich folgendermaßen beschreiben:
-
Wenn man (in Gedanken) mit dem Fahrrad den Graph von links nach rechts (also von negativen zu positiven x-Werten) und den Lenker nach rechts einschlägt, hat der Graph Rechtskrümmung bzw. ist konkav.
-
Muss man den gedanklichen Fahrradlenker nach links einschlagen, hat der Graph Linkskrümmung bzw. ist konvex.
-
Hält man den Lenker gerade, ist auch der Graph eine Gerade und der Graph hat die Krümmung 0.
Mithilfe der zweiten Ableitung \(f''(x)\) der betrachteten Funktion (sofern diese existiert), kann man die Krümmrichtung des Funktionsgraphen bestimmen. Bei Rechtskrümmung ist \(f''(x)<0\), weil die erste Ableitung, d. h. die Steigung des Graphen, abnimmt. Umgekehrt nimmt die Steigung des Graphen bei Linkskrümmung zu, daher ist dann \(f''(x)>0\). Bei \(f''(x)=0\) ist die Steigung konstant, was genau der Definition einer Geraden entspricht.
Das Krümmungsverhalten eines Graphen ist ein Kriterium zur Beurteilung, ob an einer Extremstelle ein Maximum oder ein Minimum vorliegt:
-
An einem Maximum herrscht immer Rechstkrümmung (\(f''(x)<0\)),
-
an einem Minimum immer Linkskrümmung (\(f''(x)>0\)).