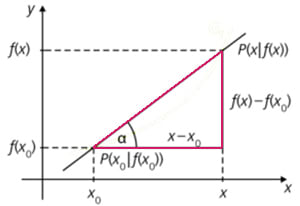
Die Steigung einer Geraden im Koordinatensystem ist das Verhältnis \(\dfrac{\Delta y}{\Delta x} = \dfrac{\Delta f(x)}{\Delta x}=\dfrac{f(x) - f(x_0)}{x-x_0}\). Sie entspricht dem Tangens des Steigungswinkels \(\alpha\) und dem Parameter m in der allgemeinen Gleichung einer linearen Funktion, y = f(x) = mx + b:
\(\dfrac{\Delta y}{\Delta x} = \tan \alpha = m\)
Anmerkung: Das Dreieck mit den Seiten \(\Delta x\), \(\Delta y = \Delta f(x)\) und dem entsprechenden Geradenabschnitt heißt Steigungsdreieck.
Bei beliebigen, d. h. im Allgemeinen nichtlinearen differenzierbaren Funktionen kann man ebenfalls von einer Steigung sprechen, diese ist dann aber im Allgemeinen an jedem Punkt des Definitionsbereichs eine andere. Man versteht in diesem Fall unter der Steigung der Funktion f an der Stelle x0 die Steigung der Tangente im Punkt P(x0|f(x0)), also den Wert der ersten Ableitung der Funktion an dieser Stelle:
\(m_\text t (x_0) = f'(x_0)\)