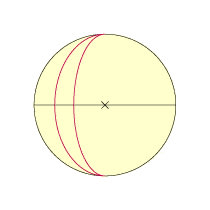
Nicht nur Kurven (insbesondere Funktionsgraphen) können gekrümmt sein, sondern auch Flächen. Ein gutes Beispiel für eine gekrümmte Fläche ist die Oberfläche der annähernd kugelförmigen Erde. Anders als in der (flachen) Ebene gelangt man, egal wohin man in gerader Richtung geht, irgendwann wieder an den Ausgangspunkt. Und anders als in der Ebene kann man der Erdoberfläche eine von geraden Seiten begrenzte Figur mit nur zwei Ecken bewundern: Solch ein Zweieck hat seine beiden Ecken am Nord- und Südpol, die Seiten sind Längenkreise (Meridiane).
Das wahrscheinlich einfachste Kriterium dafür, ob eine Fläche flach oder gekrümmt ist, ist der Winkelsummensatz im Dreieck, der nur in der Ebene gilt: Wann immer die Winkelsumme in einem (korrekt gezeichneten!) Dreieck nicht exakt 180° beträgt, ist die zugrunde liegende Fläche gekrümmt.
Übrigens: Gekrümmte Flächen mit merkwürdigen Winkelsummen im Dreieck gibt es nicht nur auf dem Globus oder in der Mathematik-AG, sondern sie spielen auch in der Relativitätstheorie von Albert Einstein ein ganz wichtige Rolle.