Unter einer Ebene versteht man in der Geometrie zweierlei: Entweder das unendlich große „Weltall“ der zweidimensionalen, flachen (euklidischen) Geometrie, also die zweidimensionale Welt, in der man Dreiecke, Kreise und andere Figuren untersucht, oder eine zweidimensionale Teilmenge des dreidimensionalen Raums.
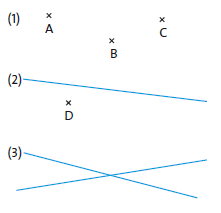
Ebenen im Raum sind durch drei Punkte festgelegt (1), deren Ortsvektoren linear unabhängig sind bzw. die nicht auf einer gemeinsamen Geraden liegen (oder komplett identisch sind). Alternativ ist eine Ebene auch durch eine Gerade und einen Punkt, der nicht auf der Geraden liegt (2), oder durch zwei verschiedene Geraden eindeutig bestimmt (3).
Ebenen können unterschiedliche Lagebeziehungen zueinander oder anderen Objekten (Geraden, Kugeln, …) haben.
Die Schnittpunkte einer Ebene mit den Koordinatenachsen nennt man Spurpunkte, je zwei Spurpunkte definieren eine Spurgerade.
In der Analytischen Geometrie beschreibt man Ebenen durch Vektor- oder Koordinatengleichungen. Man unterscheidet dabei Ebenengleichungen in Parameterform (Punkt-Richtungs-Form, Dreipunkteform) und in Koordinatenform (eng damit verwandt sind Achsenabschnittsform, Normalform und Hesse’sche Normalform). Mithilfe dieser Gleichungen kann u. a. auch der Abstand einer Ebene von einem Punkt, einer Geraden oder einer anderen Ebene berechnet werden.