Bei einer Reihe von einfachen Körpern ist es sinnvoll, eine Seitenfläche als „Grundfläche“ auszuzeichnen. Die Ausdehnung senkrecht zur Grundfläche G ist dann die Höhe h dieses Körpers. Dies ist bei zwei Arten von Körpern möglich:
- Bei Prisma und Zylinder gibt es zwei parallele, kongruente Flächen, die Grund- und die Deckfläche (welche man als „unten“ und welche als „oben“ ansieht, ist dabei egal). Beim Prisma ist die Grundfläche ein Polygon (Vieleck), beim Zylinder ein Kreis. Für das Volumen von Prisma und Zylinder gilt die einfache Merkregel „Grundfläche mal Höhe“, also V = G · h (unabhängig davon, ob es sich um einen schiefen oder einen geraden Körper handelt)
- Bei Pyramide und Kegel gibt es nur eine Grundfläche. Alle Punkte auf dem Umfang dieser Grundfläche sind mit einem darüber (oder darunter) liegenden Punkt verbunden, der Spitze der Pyramide bzw. des Kegels. Bei der Pyramide ist die Grundfläche ein Polygon (Vieleck), beim Kegel ein Kreis. Für das Volumen von Pyramide und Kegel gilt die einfache Merkregel „Grundfläche mal Höhe durch drei“, also \(V = \displaystyle \frac 1 3 \cdot g \cdot h\) (unabhängig davon, ob es sich um einen schiefen oder einen geraden Körper handelt)
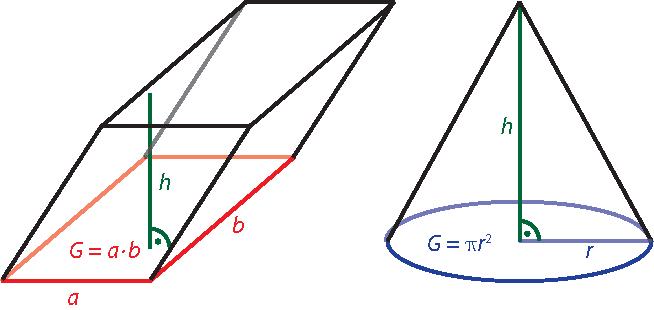
Die folgende Abbildung zeigt die Grundfläche eines schiefen Prismas mit rechteckiger Grundfläche (eine Form eines Parallelepipeds, links) und die eines geraden Kreiskegels (rechts).