Eine Pyramide ist im Allgemeinen ein Polyeder, das aus einem Polygon, der sog. Grundfläche, besteht, dessen Ecken alle mit einem gemeinsamen Endpunkt, der Spitze der Pyramide, verbunden sind. Diese Verbindungslinien werden manchmal Seitenkanten oder Mantelinien genannt. Das Lot von der Spitze auf die Grundfläche ist die Höhe h der Pyramide. Die Seitenflächen sind alle Dreiecke. Zusammengenommen bilden die Seitenflächen die Mantelfläche.
Man kann eine Pyramide auch als „eckigen Kegel“ auffassen; das Volumen einer beliebigen Pyramide berechnet sich nach der gleichen Faustformel wie beim Kegel: „Grundfläche mal Höhe durch drei“:
\(V = \displaystyle \frac 1 3 G\cdot h\)
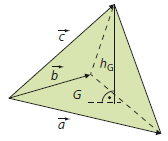
Man kann für die Volumenberechnung auch die Analytische Geometrie zu Hilfe nehmen. So gilt für das Volumen einer dreiseitigen Pyramide, die von den Vektoren \(\overrightarrow{a} , \overrightarrow{b} , \overrightarrow{c}\) aufgespannt wird („det“ steht dabei für die Determinante der Matrix mit den Spaltenvektoren \(\overrightarrow{a} , \overrightarrow{b} , \overrightarrow{c}\)):
\(\displaystyle V = \frac{1}{6} \cdot \left| \overrightarrow{a} \circ ( \overrightarrow{b} \times \overrightarrow{c} ) \right| = \frac{1}{6} \cdot \left| \det ( \overrightarrow{a} , \overrightarrow{b} , \overrightarrow{c} ) \right|\)
Wenn die Grundfläche einen definierten Mittelpunkt M hat (z. B. Diagonalenschnittpunkt in einem regelmäßigen Sechseck oder Schwerpunkt eines gleichseitigen Dreiecks), unterscheidet man zwischen geraden und schiefen Pyramiden, je nachdem, ob die Spitze senkrecht über M liegt oder nicht. Mit anderen Worten, M ist bei einer geraden Pyramide der Höhenfußpunkt, bei einer schiefen dagegen nicht.
Eine Pyramide mit einem regelmäßigen Polygon (n-Eck) nennt man auch eine regelmäßige n-seitige Pyramide, die Grundfläche wird bei dieser Ausdrucksweise nicht als „Seite“ mitgezählt.
Ist die Grundfläche ein gleichseitiges Dreieck, das mit den dann drei Seitenflächen kongruent ist, heißt der Körper Tetraeder.
Im engeren Sinn versteht man unter einer Pyramide meistens vierseitige Pyramide mit rechteckiger oder quadratischer Grundfläche, wie die Pyramiden im alten Ägypten. Die Seitenflächen einer geraden vierseitigen Pyramide sind gleichschenklige Dreiecke. Die Seitenkante s, die Höhe und die halbe Diagonalen \(\overline{AC} = e\) bzw. \(\overline{BD} = f\) der Grundfläche bilden zusammen ein rechtwinkliges Dreieck, das senkrecht auf der Grundfläche steht (Abbildung unten). Mit dem Satz des Pythagoras gilt dann
\(\displaystyle h = \sqrt{s^2-\frac 1 2 e^2} = \sqrt{s^2-\frac 1 2 f^2}\)
Man kann noch weitere rechtwinklige Dreiecke in der vierseitigen, insbesondere der quadratischen Pyramide definieren, womit sich die Mantelfläche und damit die Oberfläche bestimmen lässt.
Schneidet man eine Pyramide parallel zur Grundfläche G durch, erhält man eine kleinere Pyramide und einen Pyramidenstumpf. Die Seitenflächen eines rechteckigen bzw. quadratischen Pyramidenstumpfes sind Trapeze.
Das Volumen des Pyramidenstumpfs ist das Volumen der urpsrünglichen Pyramide minus das der kleinen Pyramide auf der Schnittfläche:
\(\displaystyle V_\text{Stumpf} = \frac 1 3 \left( G \cdot h - G_\text{Schnitt} \cdot \Delta h \right)\)