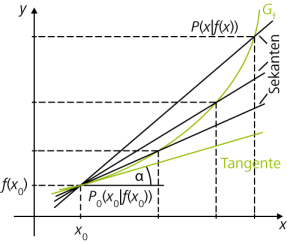
Die Ableitung einer Funktion an einer Stelle \(x_0 \in Df\) kann man sich bildlich als den Grenzwert der Sekantensteigungen vorstellen, wenn man den Abstand zwischen den beiden Schnittpunkten von Funktionsgraph und Sekante gegen null gehen lässt. Die Sekantensteigung ms ist definiert als
\(m_\text s = \dfrac {f(x)-f(x_0)}{x-x_0} = \dfrac {\Delta f(x)}{\Delta x}\)
und wird als Differenzenquotient bezeichnet. Lässt man x gegen x0 gehen, wird die Sekantensteigung zur Tangentensteigung mt, also zur Steigung der Tangente an Gf im Punkt P0(x0|f(x0)) und der Differenzenquotient wird zum Differenzialquotienten:
\(\displaystyle m_\text t = \lim_{x \to x_0} \dfrac {f(x)-f(x_0)}{x-x_0} = \dfrac {\text d f(x)}{\text d x} = f'(x_0)\)
Setzt man die Differenz x – x0 = h, so erhält man die sogenannte „h-Form“ der Ableitung:
\(\displaystyle f'(x_0 ) = \lim_{h \to 0}\frac{f ( x_0 + h) - f ( x_0 )}{h}\).