Ein Wechselstromkreis ist ein Stromkreis, bei dem sich Stromstärke und Spannung periodisch ändern, man spricht daher von Wechselstrom und Wechselspannung. Für Wechselspannung verwendet man häufig das Symbol U~. Nach der engl. Bezeichnung „alternating current“ benutzt man für Wechselstrom auch die Abkürzung AC.
Typische Elemente eines Wechselstromkreises sind eine Energiequelle, welche die Wechselspannung liefert, Ohm’sche Widerstände, Spulen und Kondensatoren. Meist ändern sich Stromstärke und Spannung (annähernd) sinusförmig, es gilt dann:
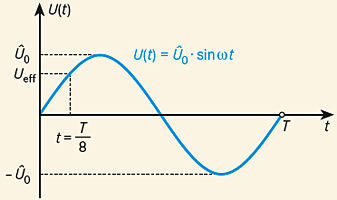
\(I(t) = \hat I\cdot \sin \omega t \\ U(t) = \hat U\cdot \sin (\omega t + \varphi)\)
I(t) und U(t) sind die Momentanwerte von Wechselstrom bzw. Wechselspannung, \(\hat I\) und \(\hat U\) die Scheitelwerte oder Amplituden. Die Größe \(\omega = 2\pi f = 2\pi/T\) (f: Frequenz, T: Schwingungsdauer/Periode) ist die Kreisfrequenz des Wechselstroms und \(\varphi\) die Phasenverschiebung zwischen Strom und Spannung. Ueff (und entsprechend Ieff) sind die sog. Effektivwerte von Spannung und Strom. Eine Gleichspannung bzw. ein Gleichstrom mit diesen Werten würde dieselbe elektrische Leistung aufnehmen.
Stromstärke und Spannung führen also Schwingungen mit gleicher Frequenz aus, sind aber i. A. phasenverschoben, etwa wenn sich Spulen oder Kondensatoren im Stromkreis befinden. Die Frequenz von technischem Wechselstrom (Netzstrom) beträgt in Deutschland 50 Hz, in den USA meist 60 Hz, viele Eisenbahnen verwenden die Frequenz 162/3 Hz. Die Netzspannung beträgt in Deutschland 230 V, in den USA 110 V. Eine besondere Form des Wechselstroms ist der Dreiphasen- oder Drehstrom,
Die Wirkungen von (Ohm’schen) Widerständen R, Kondensatoren (Kapazität C) und Spulen (Induktivität L) kann man im Wechselstromkreis zu einem Wechselstromwiderstand (einer Impedanz) Z zusammenfassen. In diesem Zusammenhang wird ein Kondensator als kapazitiver Widerstand und eine Spule als induktiver Widerstand bezeichnet. Es gilt
\(Z = \sqrt{R^2+ \left( \omega L - \dfrac 1 {\omega C} \right)^2 }\)
Dabei bezeichnet man den Bestandteil \(\left( \omega L - \dfrac 1 {\omega C} \right)\) als Blindwiderstand X und den Ohm’schen Widerstand R als Wirkwiderstand. Die Phasenverschiebung \(\varphi\) zwischen Strom und Spannung lässt sich ebenfalls über die verschiedenen Widerstände ermitteln:
\(\tan \varphi = \dfrac{ \omega L - 1/\omega C }{R }\)
Übrigens: Es gibt eine sehr elegante Darstellung der Größen im Wechselstromkreis mithilfe der komplexen Zahlen, dies ist aber kein Standardschulstoff. Eine weitere Möglichkeit ist die Zeigerdarstellung von Wechselstromgrößen, auch diese wird nur in wenigen Bundensländern in der Oberstufe behandelt.