Schwingungen (Oszillationen) und Wellen sind, ganz allgemein ausgedrückt, periodische Änderungen von physikalischen Größen, wobei diese bei Schwingungen unabhängig vom Ort bzw. an einem festen Ort stattfinden und sich bei Wellen durch den Raum ausbreiten (s. u.).
Bei einer mechanischen Schwingung ändert sich der Ort eines Körpers periodisch, etwa bei einem Fadenpendel, einer Geigensaite oder einer Membran. Bei einer elektromagnetischen Schwingung sind die periodisch veränderlichen Größen etwa die elektrische und magnetische Feldstärke, die elektrische Ladung oder Stromstärke bzw. Spannung. Schwingungen können an den verschiedensten Systemen beobachtet werden, etwa auch bei chemischen Reaktionen oder bei der Populationsgröße von Raubtieren und ihrer Beute.
Eine Schwingung wird durch folgende Größen beschrieben:
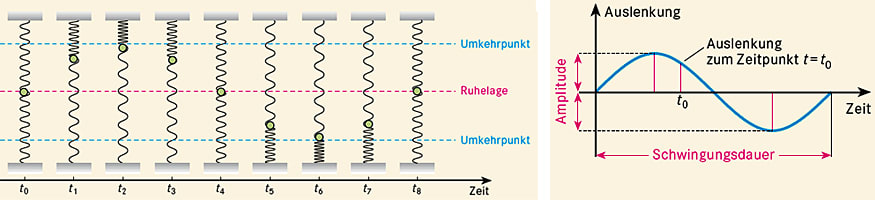
- Die Auslenkung (Elongation) ist der jeweilige Abstand des schwingenden Körpers von der Gleichgewichts- oder Ruhelage. Die Auslenkung ist also eine zeitabhängige Größe.
- Die Amplitude (Schwingungsweite) ist die maximale Auslenkung im Umkehrpunkt (genauer gesagt deren Betrag), sie ist für jeden Schwingungsvorgang eine Konstante.
- Schwingungsdauer oder Periode T: die Zeit, die für eine volle Schwingung erforderlich ist.
- Frequenz f: Anzahl der Schwingungen pro Sekunde. Es ist \(f = 1/T\).
Von zentraler Bedeutung ist die Sinusschwingung oder harmonische Schwingung. Da der Sinus auch bei einer Kreisbewegung auftritt, gibt es Entsprechungen zwischen einer Sinusschwingung und einer Kreisbewegung. Die Auslenkung y einer Sinusschwingung mit der Amplitude \(\hat y\) genügt der folgenden Gleichung:
\(y(t) = \hat y \cdot \sin(\omega t + \varphi_0)\)
(\(\omega\): Kreisfrequenz, \(\varphi_0\): Phasenwinkel). Das Argument \(\omega t + \varphi_0\) der Sinusfunktion heißt auch Phase.
Die besondere Bedeutung der Sinusschwingung beruht auch darauf, dass man alle Arten von Schwingungen als Überlagerung bzw. Summe von (möglicherweise sehr vielen) Sinusfunktionen darstellen kann.
Wellen
Wenn sich in einem schwingfähigen Medium wie z. B. Wasser, Luft oder ein Kette von gekoppelten Pendeln der Schwingungszustand der einzelnen Oszillatoren oder Schwinger räumlich ausbreitet, spricht man von einer Welle. Man kann eine Welle auch als einen sich räumlich fortpflanzenden Bewegungs- oder Erregungszustand beschreiben. Eine wesentliche Eigenschaft von Wellen ist, dass sie Energie (z. B. Bewegungsenergie) transportieren, aber niemals Materie!
Nicht jede Welle muss allerdings ein Ausbreitungsmedium wie im obigen Beispiel besitzen. Bei elektromagnetischen Wellen (und auch bei Gravitationswellen) schwingen im Vakuum definierte Felder – diese Erkenntnis hat wesentlich zur Entwicklung der Relativitätstheorie beigetragen.
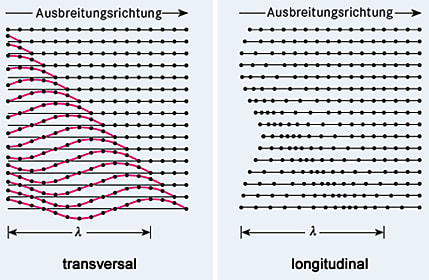
Zu den Größen Amplitude und Frequenz tritt bei Wellen noch eine dritte Grundgröße, die Wellenlänge \(\lambda\). Diese gibt an, nach welcher Entfernung sich das Schwingungsmuster wiederholt. Sie ist sozusagen das räumliche Äquivalent zur Frequenz. Für eine Sinuswelle gilt:
\(y(x,\,t) = \hat y \cdot \sin\left[ 2\pi \left(f t + \dfrac x \lambda\right)+ \varphi_0\right] = \hat y \cdot \sin(\omega t + kx+ \varphi_0)\)
dabei ist \(k = \dfrac {2\pi}\lambda\) die Kreiswellenzahl (in drei Dimensionen heißt \(\vec k = 2\pi \left(\dfrac 1 {\lambda_x},\dfrac 1 {\lambda_y},\dfrac 1 {\lambda_z} \right)\) Wellenvektor, dieser Vektor zeigt immer in Ausbreitungsrichtung der Welle).
Eine wichtige Unterscheidung ist die zwischen Transversalwellen (Auslenkung senkrecht zur Wellenausbreitung, z. B. beim Licht) und Longitudinalwellen (Auslenkung parallel zur Wellenausbreitung, z. B. bei Schall in Luft, Abb.). Transversalwellen, deren Schwingungsrichtung immer in dieselbe Raumrichtung weist, nennt man polarisiert.
Das Produkt aus Frequenz und Wellenlänge ist die Ausbreitungsgeschwindigkeit c:
\(c = \lambda \cdot f = \dfrac \omega k\)
Diese Gleichung gilt in dieser einfachen Form allerdings nur dann, wenn die Ausbreitungsgeschwindigkeit unabhängig von der Frequenz und der Wellenlänge ist, wenn also keine Dispersion auftritt. Andernfalls muss man zwischen der jeweils frequenzabhängigen Phasengeschwindigkeit \(c_\text{Ph}(\omega)\) und der Gruppengeschwindigkeit \(c_\text{g}(\omega)\) unterscheiden. \(c_\text{Ph}(\omega)\) ist die Geschwindigkeit, mit der sich eine Auslenkung bzw. eine bestimmte Schwingungsphase fortpflanzt, \(c_\text{g}(\omega) = \dfrac {\text d \omega}{\text d k}\) ist die Geschwindigkeit, mit der sich ein lokalisiertes Wellenpaket fortbewegt und mit der eine W. Informationen übertragen kann. Während unter gewissen Bedingungen die Phasengeschwindigkeit einer Welle die Lichtgeschwindigkeit übersteigen kann, ist die Gruppengeschwindigkeit immer kleiner oder gleich der Lichtgeschwindigkeit im Vakuum. Bei elektromagnetischen W. im Vakuum (und in guter Näherung auch in Luft) gilt \(c_\text{Ph} = c_\text{g}\), ebenso bei Schallwellen in Luft.
Die meisten W. lassen sich durch lineare Gleichungen beschreiben, in diesem Fall gilt das Superpositionsprinzip: Wellen durchdringen sich ungestört, bei der Überlagerung von Wellen kann es an bestimmten Punkten zur Verstärkung oder Auslöschung kommen (Interferenz). Mithilfe des Huygens’schen Prinzips lassen sich Phänomene wie Beugung, Reflexion und Brechung von Wellen verstehen. Wenn eine Welle an einer Grenzfläche reflektiert wird und sich reflektierte und einfallende Welle überlagern, kann es zur Bildung von stehenden Wellen kommen.
Die wichtigsten Wellenarten sind – neben den elektromagnetischen Wellen – Schallwellen, Wasserwellen, Erdbebenwellen und Materiewellen. Wellenphänomene treten aber auch bei Menschenansammlungen (z. B. in Fußballstadien – „la ola“ heißt auf Spanisch „die Welle“), Aktienkursen und Verkehrsstaus auf. In der Quantentheorie verschwindet die klare Trennung zwischen Wellen und Teilchen (Welle-Teilchen-Dualismus).