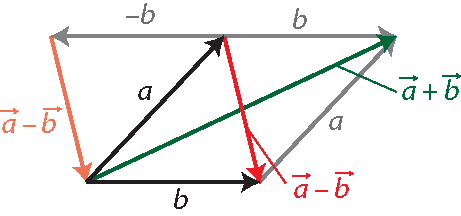
Man kann Vektoren addieren und subtrahieren. Dies kann man entweder komponentenweise definieren (siehe unten), oder grafisch (Abbildung).
- Man addiert zwei Vektoren, indem man den Startpunkt des einen an die Spitze des anderen legt. Der Summenvektor verläuft dann vom Startpunkt des ersten zur Spitze des zweiten Vektors.
- Den Differenzvektor erhält man, indem man den Gegenvektor addiert, so wie man eine Zahl subtrahiert, indem man ihre Gegenzahl addiert.
Wenn man einen Vektor und seinen Gegenvektor addiert bzw. einen Vektor von sich selbst subtrahiert, erhält man den Nullvektor: \(\vec a - \vec a = \vec a + (-\vec a) = \vec 0\). Der Nullvektor hat die Länge 0 und daher als einziger Vektor auch keine Richtung. Der Vektorpfeil über dem Nullvektor wird deshalb öfters auch weggelassen.
Wie bei normalen Zahlen gelten auch für die Vektoraddition
- das Kommutativgesetz: \(\vec a + \vec b = \vec b + \vec a\) und
- das Assoziativgesetz: \(\vec a + (\vec b + \vec c) = (\vec a + \vec b) + \vec c\).
Bei der Multiplikation ist es dagegen etwas komplizierter als bei normalen Zahlen. Es gibt die skalare Multiplikation (Zahl mal Vektor, ergibt einen Vektor), das Skalarprodukt (Vektor mal Vektor, ergibt eine Zahl) und das Kreuzprodukt bzw. Vektorprodukt (Vektor mal Vektor, ergibt einen Vektor, der auf den beiden anderen Vektoren senkrecht steht). Der Ausdruck „Skalar“ ist dabei einfach eine in der Vektorrechnung gebräuchliche andere Bezeichnung für eine gewöhnliche Zahl.
Ein Vektor, dessen Betrag bzw. Länge genau 1 ist, heißt Einheitsvektor der jeweiligen räumlichen Richtung. Man kann einen beliebigen Vektor zu einem Einheitsvektor machen, indem man ihn skalar mit dem Kehrwert seines Betrags malnimmt (bzw. skalar durch seinen Betrag teilt): \(\displaystyle \vec a^0 \equiv \hat a = \frac 1 {|\vec a|} \cdot \vec a\). \(| \hat a |= 1\). Diese Operation nennt man auch normieren, ein Einheitsvektor ist also ein „normierter Vektor“.
Da man mit Vektoren ganz ähnlich wie mit Zahlen rechnen kann, besitzt eine Vektormenge auch eine besondere mathematische Struktur, ähnlich wie der Körper der reellen Zahlen. Genauer gesagt bezeichnet man eine Menge von Vektoren als einen Vektorraum, wenn man die Vektoren wie oben dargestellt addieren kann, es eine skalare Multiplikation (z. B. mit reellen Zahlen) gibt und der Nullvektor als neutrales Element der Addition enthalten ist.
Eine Linearkombination von Vektoren ist die Summe der Vektoren, wobei jeder Vektor noch mit einem skalaren Vorfaktor (Koeffizient) multipliziert werden kann. Mithilfe von Linearkombinationen kann man überprüfen, ob die Vektoren linear abhängig oder unabhängig sind.
Wenn man jeden Vektor eines Vektorraums eindeutig als eine Linearkombination aus n linear unabhängigen Vektoren darstellen kann, bilden diese Vektoren eine Basis des Vektorraums. Die Koeffizienten der Linearkombination heißen dann die Koordinaten des Vektorraums. Der letzte Satz klingt komplizierter, als er ist: Der normale dreidimensionale Raum \(\mathbb R^3\), in dem man in der Schule räumliche Analytische Geometrie betreibt, hat als Basis die drei Einheitsvektoren in Richtung der Koordinatenachsen: \(\vec e_x\), \(\vec e_y\) und \(\vec e_z\) oder auch : \(\vec e_1\), \(\vec e_2\) und \(\vec e_3\) (es ist egal, womit man die Basisvektoren durchnummeriert.) In der zweidimensionalen Ebene gibt es zwei Basisvektoren, allgemein hat eine Basis immer so viele Basisvektoren, wie der Vektorraum Dimensionen hat.
Jeder Vektor und damit auch jeder Punkt im Raum lässt sich also als Linearkombination der drei Basisvektoren schreiben. Beispielsweise gilt für den Punkt P(2|–1|4,5): \(\vec p = 2 \cdot \vec e_1 - 1 \cdot \vec e_2 - 4,5 \cdot \vec e_3\). Deshalb schreibt man den Vektor \(\vec p\) auch als ein Zahlentripel aus diesen drei Koordinaten, die man bei Vektoren oft auch Komponenten nennt: \(\vec p = \begin{pmatrix} 2 \\ -1 \\ 4,5 \end{pmatrix}\).
Achtung: Auch wenn „Punkt im Raum“ und „Vektor mit drei Komponenten“ das Gleiche zu sein scheinen, gibt es Unterschiede. Korrekt muss man sagen, dass der Vektor \(\vec p\) der Verbindungsvektor zwischen dem Koordinatenursprung und dem Punkt P ist, man nennt ihn auch den Ortsvektor von P. Wichtig ist auch, dass es von dem gewählten Koordinatensystem abhängt, also z. B. davon, welchen Punkt man als Nullpunkt bzw. Ursprung wählt, welche Zahlen die Komponenten eines Vektors bilden.
Hat man sich einmal für ein Koordinatensystem entschieden und damit die Komponenten der Vektoren eindeutig festgelegt, kann man die Rechenregeln der oben beschriebenen Operationen auch in Komponentenform angeben. Für Addition, Subtraktion und Multiplikation mit dem Skalar \(r \in \mathbb R\) von zwei Vektoren \(\vec a = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\) und \(\vec b = \begin{pmatrix} b_1 \\ b_2\end{pmatrix}\) bzw. \(\vec a = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\) und \(\vec b = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}\) gilt: