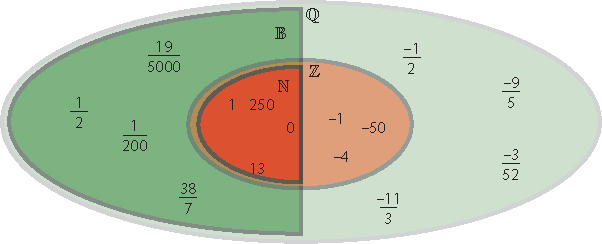
Die Menge \(\mathbb{Q}\) der rationalen Zahlen enthält alle Bruchzahlen und ihre Gegenzahlen. Anders ausgedrückt sind die rationalen Zahlen die Brüche mit ganzen Zahlen in Zähler und Nenner:
\(\mathbb{Q} = \left\{ x \left| x = \dfrac s t,\ s,t \in \mathbb Z \right. \right\}\)
In der Menge \(\mathbb{Q}\) sind die Mengen \(\mathbb N\), \(\mathbb B\) und \(\mathbb Z\) der natürlichen, ganzen und Bruchenzahlen enthalten.
Anmerkung: Da man einen Bruch erweitern oder kürzen kann, ohne dass sich ein Wert ändert, ist die Darstellung einer rationalen Zahl als Bruch nicht eindeutig. Um Eindeutigkeit zu erreichen, müsste man noch verlangen, dass die Brüche jeweils vollständig gekürzt sind.
In der Menge der rationalen Zahlen führt jede der vier Grundrechenarten immer auf ein Ergebnis innerhalb der Menge. Es ist allerdings nicht möglich, die Wurzel aus einer rationalen Zahl zu ziehen, die keine Quadratzahl (oder ein Quotient aus Quadratzahlen) ist.
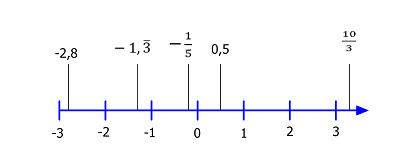
Man kann die rationalen Zahlen auf der Zahlengeraden darstellen, allerdings entsprechen nicht alle Punkte auf der Zahlengeraden auch einer rationalen Zahl. Tatsächlich liegen sogar zwischen zwei rationalen Zahlen immer unendlich viele irrationale Zahlen. Erst die reellen Zahlen enthalten alle Punkte auf der Zahlengerade.