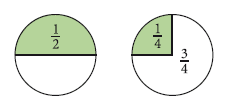Der Begriff „Bruch“ wird in der Mathematik in mehreren, leicht verschiedenen Bedeutungen gebraucht:
-
Ein Bruch ist zunächst einfach eine andere Schreibweise für eine Division, denn man kann statt „a : b“ immer auch „\(\dfrac a b\)“ schreiben. Dabei ist a jeweils der Dividend (das, was geteilt wird) und b der Divisor (das, wodurch geteilt wird). Die Zahl über dem Bruchstrich heißt In Bruchschreibweise Zähler, die Zahl unter dem Bruchstrich ist der Nenner. Das Ergebnis der Division (der Quotient oder das Verhältnis) wird dann einfach „Bruch“ genannt.
Anmerkung: Man kann auf sehr einfache Weise das Ergebnis jeder noch so beliebigen Division angeben: indem man es einfach als Bruch schreibt! -
Jeder Bruch ist eine Darstellung einer Bruchzahl. Brüche, die man durch Erweitern oder Kürzen ineinander umwandeln kann, stellen dieselbe Bruchzahl dar. Oft werden deshalb Brüche, deren Zähler und Nenner Zahlen sind (und keine Terme mit Variablen) als Bruchzahlen angesehen bzw. umgekehrt Bruchzahlen „Brüche“ genannt.
-
Schließlich bezeichnet man oft auch Bruchterme (z. B. den Funktionsterm einer gebrochenrationalen Funktion) kurz als Brüche.
Weitere Bezeichnungen:
- Der Bruch \(\dfrac{b}{a}\) ist der Kehrwert (das Reziproke) des Bruches \(\dfrac{a}{b}\).
-
Bei echten Brüchen (einfachen Brüchen, gemeinen Brüchen) ist der Zähler betragsmäßig kleiner als der Nenner, sie stellen also eine Bruchzahl zwischen 0 und ±1 dar, Beispiel: \(\dfrac 2 3\).
Echte Brüche geben den Anteil an einem Ganzen an. Der Nenner gibt die Zahl der Teile an, der Zähler gibt an, wie viele dieser Teile den Wert des Bruchs ausmachen. -
Ein Stammbruch hat den Zähler ±1, Beispiel: \(\dfrac 1 {13}\).
-
Ein Bruch mit dem Nenner ±1 ist eine natürliche bzw. ganze Zahl und wird manchmal als Scheinbruch bezeichnet, Beispiel: \(\dfrac 4 1=4\). Erweiterte Scheinbrüche sind auch Scheinbrüche, etwa \(\dfrac {12} 3\) oder \(\dfrac {1000} {10}\).
-
Unechte Brüche sind (betragsmäßig) größer als 1, haben also einen größeren Zähler als Nenner. Man kann jeden unechten Bruch auch als gemischte Zahl (gemischten Bruch) schreiben, also als Summe aus einer ganzen Zahl und einem echten Bruch:
\(\dfrac {14} {11}= 1+ \dfrac 3{11} = 1 \dfrac 3{11}\) -
Ein Dezimalbruch hat eine Zehnerpotenz im Nenner und kann als abbrechende Dezimalzahl geschrieben werden, Beispiel: \(\dfrac 7 {10}; \ \dfrac {394} {10.000}\).