Mathematik
5. Klasse
‐
Abitur
Polarkoordinaten
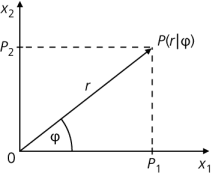
Statt durch kartesische Koordinaten Punkts Polarkoordinaten angegeben werden. Deren Komponenten sind der Abstand r vom Ursprung und der Winkel \(\varphi\) , den sein Ortsvektor mit der waagerechten Koordinatenachse (x -Achse bzw. x 1 -Achse) bildet. Dabei ist r eine nicht negative reelle Zahl und \(\varphi\) ein Winkel zwischen 0° und 360°, im Bogenmaß \(2\pi\) .
Für die kartesischen Koordinaten des Punkts P(P 1 |P 2 ) gilt:
\(P_1 = r \cdot \cos \varphi\)
\(P_2 = r \cdot \sin \varphi\)
Das dreidimensionale Gegenstück zu den Polarkoordinaten sind die Kugelkoordinaten
Zugehörige Videos und Aufgaben
Registriere dich kostenlos und nutze für 2 Tage die PremiumPlus Flat mit allen Funktionen
Übungen, Klassenarbeiten und mehr testen
Jetzt 2 Tage testen
Zugehörige Klassenarbeiten
Ein Blatt DIN-A4-Papier liegt in der \(x_1\) - \(x_2\) -Ebene. Gegeben sind seine Eckpunkte \(O(0|0|0)\) , \(A(\sqrt{2}|0|0)\) , \(B(\sqrt{2}|1|0)\) und \(C(0|1|0)\) sowie der Punkt \(D(1|1|0)\) . (Als Längeneinheit (LE) wird die Länge der kürzeren Seite des DIN-A4-Blattes verwendet.) Das Blatt wird jetzt entlang der Strecke \(\overline {OD}\) gefaltet. Das Dreieck \(ODC\) bleibt dabei fest, während das Viereck \(OABD\) in das Viereck \(OA'B'D\) übergeht, das wieder in der \(x_1\) - \(x_2\) -Ebene liegt. Die Gegebenheiten sind in den folgenden Schrägbildern dargestellt. Zur
Die Entwicklung der Population einer bestimmten Seevogelart in einem festgelegten Beobachtungsgebiet wird durch folgende Modellannahmen beschrieben: Die Überlebensrate der Vögel in den ersten beiden Lebensjahren wird jeweils mit \(0{,}6\) angenommen, in den späteren Lebensjahren mit \(0{,}8\) . Die erste Brut findet im 3. Lebensjahr statt, der Bruterfolg wird mit \(0{,}5\) Jungvögeln pro Elternvogel und Jahr angenommen. Die Vögel werden in 3 Altersgruppen eingeteilt, deren Anzahlen \(x_1\) : Anzahl der Jungvögel im 1. Lebensjahr (Altersgruppe 1) \(x_2\) : Anzahl der Vögel im 2. Lebensjahr
Die Lösungsvorschläge liegen nicht in der Verantwortung des jeweiligen Kultusministeriums.
Die Entwicklung der Population einer bestimmten Seevogelart in einem festgelegten Beobachtungsgebiet wird durch folgende Modellannahmen beschrieben: Die Überlebensrate der Vögel in den ersten beiden Lebensjahren wird jeweils mit \(0{,}6\) angenommen, in den späteren Lebensjahren mit \(0{,}8\) . Die erste Brut findet im 3. Lebensjahr statt, der Bruterfolg wird mit \(0{,}5\) Jungvögeln pro Elternvogel und Jahr angenommen. Die Vögel werden in 3 Altersgruppen eingeteilt, deren Anzahlen \(x_1\) : Anzahl der Jungvögel im 1. Lebensjahr (Altersgruppe 1) \(x_2\) : Anzahl der Vögel im 2. Lebensjahr
