Ein Parallelogramm ist ein Viereck, bei dem sich gegenüberliegende Seiten zueinander parallel sind (daher der Name). Dies ist nur möglich, wenn die parallelen Seitenpaare auch jeweils gleich lang sind.
Ein Parallelogramm hat die folgenden weiteren Eigenschaften:
- Je zwei gegenüberliegende Winkel sind gleich groß.
- Benachbarte Winkel ergänzen sich zu 180°.
- Die Diagonalen halbieren sich.
- Das Parallelogramm ist punktsymmetrisch bezüglich des Diagonalenschnittpunkts, es hat aber keine Achsensymmetrie.
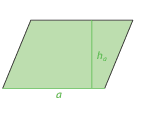
Schneidet man ein Parallelogramm entlang der Höhe über einer Seite in zwei Teile, so lassen sich die beiden Teilflächen zu einem Rechteck zusammenfügen.
An dieser Skizze liest man direkt ab, dass der Flächeninhalt des Parallelogramms gleich dem des zurechtgeschobenen Rechtecks ist, also:
\(A_\text{Parallelogramm} = a \cdot h_a = b \cdot h_b\).
Aus dieser Formel folgt, dass die Fläche eines Parallelogramms gleich bleibt, wenn man eine Seite parallelverschiebt (da sich dadurch die Höhe nicht ändert).
In der Analytischen Geometrie kann man diesen Flächeninhalt des Parallelogramms ABCD auch mithilfe des Kreuzprodukts der Verbindungsvektoren zwischen den Eckpunkten berechnen:
\(A = \left| \overrightarrow{AB} \times \overrightarrow{AD} \right| = \left| \overrightarrow{AB} \right| \cdot \left| \overrightarrow{AD} \right| \cdot \sin \alpha\)