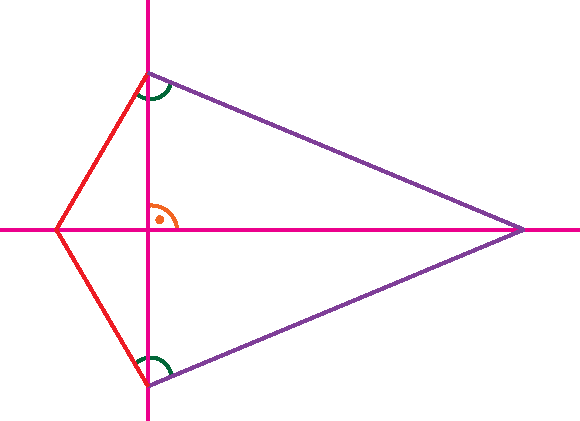
Ein Drachenviereck ist ein Viereck, bei dem jeweils zwei benachbarte Seiten gleich lang sind – etwa so wie bei einem Papierdrachen, den man im Herbst steigen lässt.
Ein Drachenviereck hat die folgenden weiteren Eigenschaften:
- Die beiden Diagonalen stehen senkrecht aufeinander.
- Eine Diagonale ist Symmetrieachse.
- Die Symmetrieachse halbiert die Winkel an den Ecken, die sie verbindet. Die beiden anderen Winkel sind gleich groß.
- Das Drachenviereck hat sowohl einen Inkreis als auch einen Umkreis, ist also sowohl Tangenten- als auch Sehnenviereck.
- Der Flächeninhalt ist das halbe Diagonalenprodukt: A=e⋅f2.
