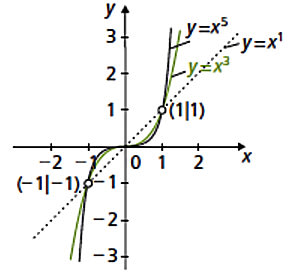Zwei Funktionsgraphen berühren sich, besitzen also einen Berührpunkt PB(xB|yB), wenn die zugehörigen Funktionen f und g an diesem Punkt sowohl gleiche Funktionswerte als auch gleiche Werte der ersten Ableitung haben:
\(y_\text B = f(x_\text B ) = g(x_\text B )\) und \(f'(x_\text B ) = g'(x_\text B )\)
Geometrisch bedeutet das, dass PB nicht nur ein gemeinsamer Punkt der beiden Funktionen ist, sondern dass f und g dort auch die gleiche Tangente besitzen.
Beispiel:
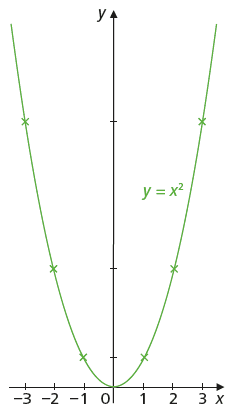
Die Normalparabel y = x2 und die x-Achse (y = 0) berühren sich im Ursprung, da \(f'(0) = 2\cdot 0 = 0\) ist.
Achtung: Ein Berührpunkt bedeutet nicht zwangsläufig, dass sich die Funktionen nicht schneiden. Beispielsweise haben die kubische Parabel y = x3 oder die Funktion y = x5 im Ursprung einen Sattelpunkt, also einen Schnittpunkt mit der x-Achse, der gleichzeitig ein Berührpunkt ist.