Das Trägheitsmoment J ist ein Maß für den Widerstand, den ein Körper der Änderung seiner Winkelgeschwindigkeit entgegensetzt. Es spielt damit bei einer Drehbewegung die gleiche Rolle wie die (träge) Masse bei einer Translationsbewegung.
Dies lässt sich herleiten, wenn man die kinetische Energie \(E_\text{kin} = \dfrac 1 2 mv^2\) eines rotierenden mit Masse m in Abhängigkeit von der Winkelgeschwindigkeit \(\omega = v/r\)ausdrückt, also seine berechnet:
\(E_\text{rot} = \dfrac 1 2 mr^2\omega^2\)
Die Dimension des T. ist somit Masse mal Länge zum Quadrat, die SI-Einheit \(\text{kg}\times\text{m}^2\).
Die Rotationsenergie Erot eines System aus n Massenpunkten mit Massen mi und dem jeweiligen (senkrechten) Abstand ri von der Drehachse, ist
\(\displaystyle E_\text{rot} = \frac 1 2 \left(\sum_{i=1}^n m_ir_i^2 \right) \omega^2 = \frac 1 2 J \omega^2\)
Die Größe in Klammern ist das Trägheitsmoment \(\displaystyle J = \sum_{i=1}^n m_ir_i^2 \).
Hat man anstatt mit n Massenpunkten mit einer kontinuierlichen Massenverteilung zu tun, muss man integrieren, im allgemeinen Fall sogar über alle drei Raumrichtungen, was den Rahmen der Schulmathematik übersteigt.
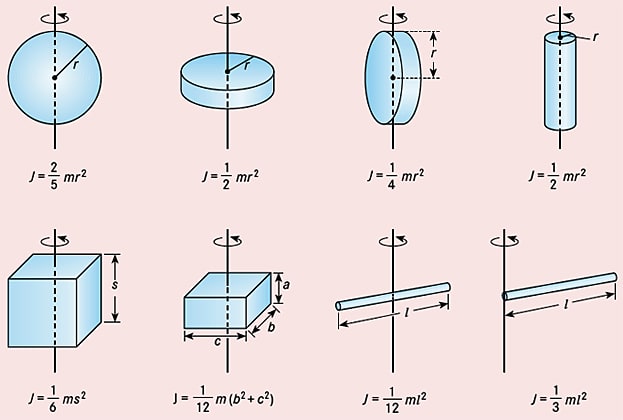
Da die Abstände ri von der Drehachse in das Trägheitsmoment eingehen, ist es immer nur bezüglich einer bestimmten Achse definiert, die jeweils mit angegeben werden muss (man erhält für dasselbe System verschiedene Trägheitsmomente, wenn man unterschiedliche Drehachsen wählt, Abb.).