Eine wichtige Eigenschaft aller natürlichen, ganzen, rationalen und reellen Zahlen (Zahlenbereiche) ist, dass man sie immer eindeutig anordnen und vergleichen kann – man weiß immer genau, wo man sie einzusortieren hat. Etwas formaler sagt man:
Für zwei Zahlen x und y gilt immer genau eine der drei folgenden Aussagen:
- x ist größer als y: x > y
- x ist gleich y: x = y
- x ist kleiner als y: x < y
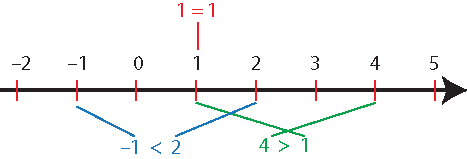
Man kann sich dies so veranschaulichen: Zwei Zahlen liegen auf der Zahlengeraden entweder an exakter derselben Stelle (gleich), oder eine von ihnen ist rechts und die andere links (größer bzw. kleiner).
Die Vergleichszeichen (Ordnungsrelationen) sind transitiv, d. h.:
Wenn x > y und y > z, dann ist x > z (ebenso: \(x = y\ \land\ y = z\ \ \Rightarrow \ \ x = z\) und \(x < y\ \land\ y < z\ \ \Rightarrow \ \ x < z\)).
Es gibt noch die folgenden weiteren Vergleichszeichen:
- „Größer (oder) gleich“: \(x \ge y \ \ \Leftrightarrow \ \ x > y \ \lor \ x = y\)
- „Kleiner (oder) gleich“: \(x \le y \ \ \Leftrightarrow \ \ x < y \ \lor \ x = y\)
- „Ungleich“: \(x \ne y \ \ \Leftrightarrow \ \ x > y \ \lor \ x<y\)
Wenn man zwei Terme mit einem Gleichheitszeichen verknüpft, bekommt man eine Gleichung, wählt man stattdessen eines der anderen Vergleichszeichen, eine Ungleichung.