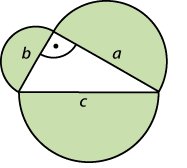
Der verallgemeinerte Pythagoras-Satz gilt für rechtwinklige Dreiecke und behandelt den Fall, dass nicht Quadrate, sondern allgemein ähnliche Figuren über Katheten und Hypotenuse betrachtet werden. In diesem lautet die Formulierung:
Wenn man über den Katheten eines rechtwinkligen Dreiecks zwei zueinander ähnliche Figuren zeichnet, dann ist die Summe ihrer Flächen so groß wie eine zu ihnen ähnliche Fläche über (bzw. unter) der Hypotenuse.
Beispiele:
Die Halbkreisflächen über den Seiten a, b und c bestimmen sich zu \(\displaystyle F_a= \frac{1}{2} \left(\frac{a}{2}\right)^2 \pi , \ F_b= \frac{1}{2} \left(\frac{b}{2}\right)^2 \pi,\ F_c= \frac{1}{2} \left(\frac{c}{2}\right)^2 \pi\) . Aus \(c^2 = a^2 + b^2\) folgt dann \(\displaystyle \frac{\pi }{8} c^2 = \frac{\pi }{8} a^2 + \frac{\pi }{8} b^2\) , d. h. \(F_c = F_a + F_b\) .