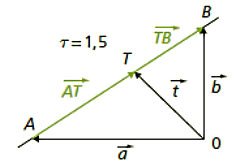
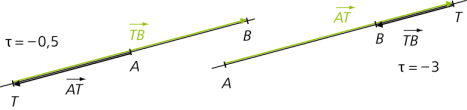
Die reelle Zahl \(\tau\), die für die drei verschiedenen Punkte A, B und T auf einer Geraden die Gleichung \(\overrightarrow{AT} = \tau \cdot \overrightarrow{TB}\) erfüllt, heißt das Teilverhältnis des Punkts T bezüglich der Strecke \(\overline{AB}\).
Für \(T \in \overline{A B}\) (innere Teilung) gilt \(\tau \geq 0\), andernfalls (äußere Teilung) ist \(\tau < 0\).