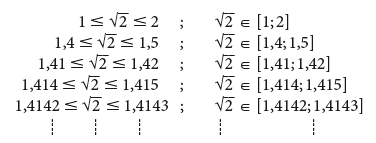Intervallschachtelungen dienen zur exakten Definition von irrationalen Zahlen bzw. allgemein von reellen Zahlen.
Eine Intervallschachtelung ist eine Folge (In) von Intervallen, wobei das nächste Glied immer im vorigen Glied der Folge enthalten ist und nur eine Zahl in allen Folgengliedern enthalten ist. Diese Zahl ist die rationale oder irrationale Zahl, welche durch diese Intervallschachtelung eindeutig festgelegt ist. Die Intervallfolge wiederum wird definert durch die monoton steigende Zahlenfolge (an) und die monoton fallende Zahlenfolge (bn), welche jeweils die Intervallgrenzen bilden. Diese beiden Folgen konvergieren zum selben Grenzwert, oder anders ausgedrückt: die Folge der Differenzen, (an – bn), also der Intervalllängen, ist eine Nullfolge.
Es gilt also:
\(I_n = [a_n;\, b_n]\); \(\displaystyle \lim_{n \to \infty}a_n = \lim_{n \to \infty}b_n = c\); \(c \in I_n \ \ (n \in \mathbb N)\)
Beispiel:
Um die irrationale Zahl \(\sqrt{2}\) zu definieren, wählt man als Intervallgrenzen jeweils zwei Dezimalbrüche mit zunehmender Zahl an Nachkommastellen, deren letzte Stelle sich um 1 unterscheidet und von denen eine kleiner und eine größer als \(\sqrt{2}\) ist.
Die Zahl \(\sqrt{2}\) wird somit durch die Intervalle \([1; 2], [1,4; 1,5], [1,41; 1,42], [1,414; 1,415]\) ... „eingeschachtelt“.