Allgemein ist der Flächeninhalt A der Figur, die von einem Funktionsgraphen Gf, der x-Achse und den senkrechten Verbindungslinien zwischen ihnen (an den Grenzen des Intervalls []) begrenzt wird, das bestimmte Integral
\(\displaystyle A = \left| \int\limits_{a}^{b} | f (x)|\, \text dx \right|\) .
Für \(a \leq b\) fallen die äußeren Betragsstriche weg. Ist \(f (x) \geq 0\) für alle \(x \in [a; b]\), fallen die inneren Betragsstriche weg. Wenn die Funktion im Intervall das Vorzeichen wechselt, muss man die sich ergebenden Teilflächen jeweils separat berechnen.
Beispiel:
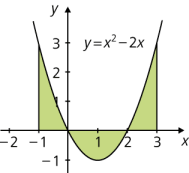
\(\displaystyle A = \int\limits_{-1}^{3} | x^2-2x|\, \text dx = \int_{-1}^{0} (x^2-2x)\, \text dx + \int_0^2\! -( x^2-2x)\, \text dx + \int_2^3 x^2-2x\, \text dx = \left[ \frac{x^3}{3} - x^2 \right]^0_{-1} - \left[ \frac{x^3}{3} - x^2 \right]^2_{0} + \left[ \frac{x^3}{3} - x^2 \right]^3_{2} = \frac{4}{3} + \frac{4}{3} + \frac{4}{3} = 4\)
Wenn der Integrationsbereich symmetrisch um den Ursprung liegt und die Integrandenfunktion gerade oder ungerade (also symmetrisch zur y-Achse oder zum Ursprung) ist, genügt es, das Integral für nur eine Hälfte des Intervalls zu lösen und dann das Ergebnis mit 2 zu multiplizieren:
\(\displaystyle A = \int_{-a}^{a} | f (x)|\, \text dx = 2 \cdot \int_{0}^{a} | f (x)|\, \text dx \ \ (a \ge 0)\)
Beispiel:
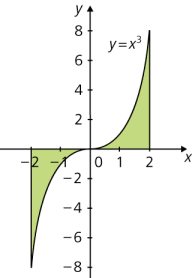
\(\displaystyle A = \int_{-2}^{2} | x^3|\, \text dx = 2 \cdot \int_{0}^{2} | x^3|\, \text dx = 2 \cdot \left[ \frac{x^4}{4} \right]^2_0 = 2 \cdot 4 = 8\)
Die Fläche zwischen zwei Graphen ist das Integral über die Differenzfunktion zwischen den Schnittpunkten der Funktionsgraphen.
\(\displaystyle A = \left| \int_a^b |f (x)\, \text dx \right| - \left|\int_a^b g (x)| \, \text dx \right| = \left| \int_a^b |f (x) - g (x)| \, \text dx \right|\)
Beispiel:
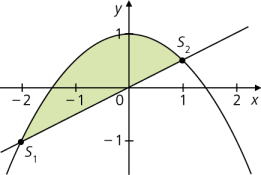
Fläche zwischen Parabel und Gerade mit \(f : x \mapsto - 0,5 x^2 + 1\) und \(g : x \mapsto 0,5x\) (\(x \in \mathbb{R}\)). Die Schnittpunkte sind S1(–2|–1) und S2(1|0,5).
\(\displaystyle A = \int_{-2}^{1} (f (x) - g(x))\, \text dx = \int_{-2}^{1} ((-0,5x^2+1)-0,5x)\, \text dx = 2,25\)