Winkelgeschwindigkeit und Kreisfrequenz sind zwei eng miteinander verwandte physikalische Größen, die bei Rotationsbewegungen bzw. Schwingungen und Wellen eine große Rolle spielen. Das Formelzeichen ist in beiden Fällen \(\omega\), die SI-Einheit ist wie bei allgemeinen Frequenzen das Hertz, es ist \(1\,\text{Hz} = \dfrac 1 {\text s}\) (man kann auch die Einheit Radiant pro Sekunde, rad/s, benutzen, da Radiant aber eine der wenigen dimensionslosen Einheiten ist, kann man sie auch gleich ganz weglassen).
Bei einer Rotation (Drehbewegung, Kreisbewegung) definiert man die Winkelgeschwindigkeit als das Verhältnis aus überstrichenem Winkel \(\Delta \varphi\) (in Bogenmaß!) und dafür benötigter Zeit \(\Delta t\):
\(\omega = \dfrac{\Delta \varphi}{\Delta t}\)
Zwischen \(\omega\), der Umlauffrequenz f und der Umlaufpriode T gilt die Beziehung:
\(\omega = 2\pi f = \dfrac{2\pi} T\)
Allgemeiner ist die Winkelgeschwindigkeit gleich der zeitlichen Ableitung des Winkels:
\(\omega = \dfrac{\text d \varphi}{\text d t} = \dot \varphi\)
Die zweite Zeitableitung des Winkels bzw. die zeitliche Ableitung der Winkelgeschwindigkeit ist die Winkelbeschleunigung \(\alpha\):
\(\alpha = \dot \omega = \ddot \varphi\)
Winkelgeschwindigkeit und Winkelbeschleunigung sind genau genommen Vektoren, deren Richtung aus der Rechte- Hand-Regel bestimmt werden kann; die Vektoren \(\vec \omega\) und \(\vec \alpha\) zeigen in die Richtung des Daumens der rechten Hand, wenn deren gekrümmte Finger in Drehrichtung weisen. Ihre Beträge entsprechen den bisher behandelten skalaren Größen \(\omega\) und \(\alpha\) .
Zusammenhang zwischen Winkelgeschwindigkeit und Kreisfrequenz
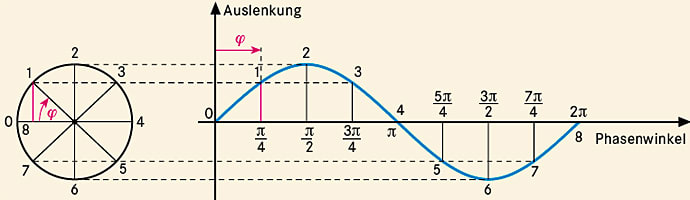
Wenn man in einem sog. Zeigerdiagramm (Abb.) den y-Wert einer Kreisbewegung gegen den überstrichenen Winkel (Phasenwinkel) aufträgt, erkennt man, dass die oben definierte Winkelgeschwindigkeit \(\omega\) gerade der Kreisfrequenz \(\omega\) im Ausdruck \(y = \sin \omega t\) einer Sinusschwingung entspricht. Anders ausgedrückt ist die Kreisfrequenz die Winkelgeschwindigkeit des Zeigers im Zeigerdiagramm.