Klassenarbeit
Physik
7.
‐
8. Klasse
Stromkreise (2)
Dauer:
45 Minuten
Ergänze folgenden Lückentext mit den richtigen Begriffen aus der am Ende gegebenen Liste. Die Begriffe können auch gar nicht oder mehrfach verwendet werden.
Ein ______________ ist ein elektrisches Bauteil, das ___________________ speichern kann. Er besteht aus zwei Platten ___________________ Material, die durch eine dünne Schicht eines sogenannten ___________________ voneinander getrennt sind. Das ist ein ___________________ , z. B. ___________________ oder ___________________ . Die Fähigkeit, ___________________ zu speichern, hängt von ___________________ und ___________________ der beiden Platten sowie von der ___________________ des ___________________ ab.
Auswahlmöglichkeiten: isolierendem / Nussnugat / Öl / Farbe / Abstand / Ladungen / Protonen / Transformator / leitendem / Dielektrikum(s) / Luft / Isolator / transparentes / Fläche / Aluminium(s) / Kondensator / Transistor(s) / Leiter / Volumen / Permittivität / Leitungswasser / Gold / Masse / Temperatur / Primitivität
Gegeben sind drei Widerstände mit den Werten 1,0 Ω, 2,0 Ω und 3,0 Ω.
Welcher Gesamtwiderstand ergäbe sich, wenn sie in Reihe geschaltet wären?
Wie groß müsste ein einzelner Widerstand sein, der diese Widerstände ersetzt, wenn sie parallel geschaltet wären?
An einen Plattenkondensator mit der Plattenfläche A = 300 cm2 und dem Plattenabstand d = 3 mm im Vakuum wird die Spannung U = 300 V angelegt.
Welche Ladung nimmt der Kondensator auf?
Welche Feldstärke hat das elektrische Feld im Kondensator?
Wie ändern sich Ladung und Feldstärke, wenn der Plattenabstand bei Beibehaltung der Verbindung zur Spannungsquelle vergrößert wird?
Wie ändern sich Ladung, Feldstärke und Spannung, wenn die Vergrößerung des Plattenabstands nach Abklemmen der Spannungsquelle erfolgt?
Du hast drei Widerstände, von denen jeder einen Einzelwiderstand von 10 Ω hat. Wie musst du sie schalten, damit der Gesamtwiderstand 15 Ω beträgt?
Zeichne ein Schaltbild.
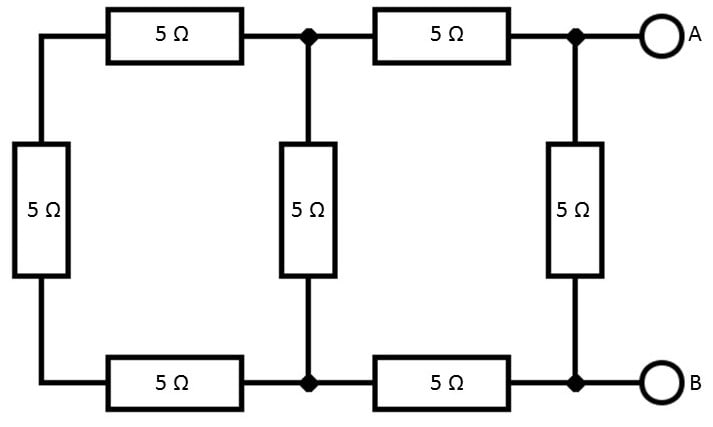
Wie groß ist der Gesamtwiderstand zwischen den Punkten A und B, wenn jeder Einzelwiderstand 5 Ω beträgt?
Benötigte Lernwege
Was ist eine Parallelschaltung?
Was ist elektrische Spannung?
Was ist elektrischer Strom und was bedeutet Stromstärke?
Registriere dich kostenlos und nutze für 2 Tage die PremiumPlus Flat mit allen Funktionen
Übungen, Klassenarbeiten und mehr testen
Hinweis Diese Klassenarbeit deckt ausschließlich das Thema "Stromkreise " ab. Üblicherweise umfasst eine Klassenarbeit mehrere Themen. Um dich gezielt darauf vorzubereiten, solltest du alle Themen bearbeiten, die ihr behandelt habt.
Wie du dich auf Klassenarbeiten vorbereitest.
So lernst du mit Klassenarbeiten:
Drucke dir eine Klassenarbeit aus.
Bearbeite die Klassenarbeit mit einem Stift und Papier wie in einer echten Klassenarbeit.
Vergleiche deine Ergebnisse mit der zugehörigen Musterlösung.