Was du wissen musst
-
Wie muss man sich Spannung vorstellen?
Dass sich Elektronen durch einen Stromkreis bewegen, liegt natürlich an dem elektrischen Feld. Anschaulich kann man sich die Situation in einer Batterie so vorstellen:
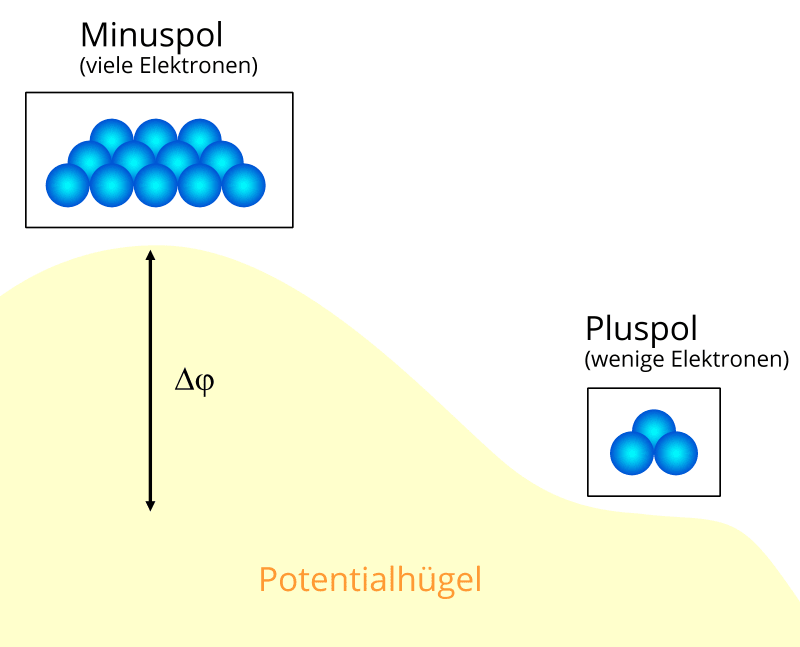
- Am Minuspol der Batterie sind viele Elektronen vorhanden. Sie sind alle negativ geladen und stoßen sich deshalb ab. Etwas genauer ausgedrückt, ist die potenzielle Energie, die sie aufgrund des elektrischen Feldes haben, groß.
- Am Pluspol gibt es wenige Elektronen, die sich deshalb weniger stark abstoßen und somit auch eine geringere potenzielle Energie besitzen.
Der Unterschied an potenzieller Energie, den ein Elektron am Minuspol im Vergleich zum Pluspol hat, hängt immer von der Ladung \(q\) des Elektrons ab. Wenn man diesen Energieunterschied durch \(q\) teilt, verschwindet diese Abhängigkeit. Genau das hat man sich bei der Definition der Potenzialdifferenz (und damit der Spannung) gedacht:
\(\begin{align} U =\Delta\varphi = - \frac{\Delta E_{pot}}{q} \end{align}\)
Damit ist die Potenzialdifferenz eine gute Größe, um das elektrische Feld zu beschreiben, weil sie (im Gegensatz zur potenziellen Energie) nicht von der Ladung \(q\) des Teilchens abhängt, das man gerade betrachtet.
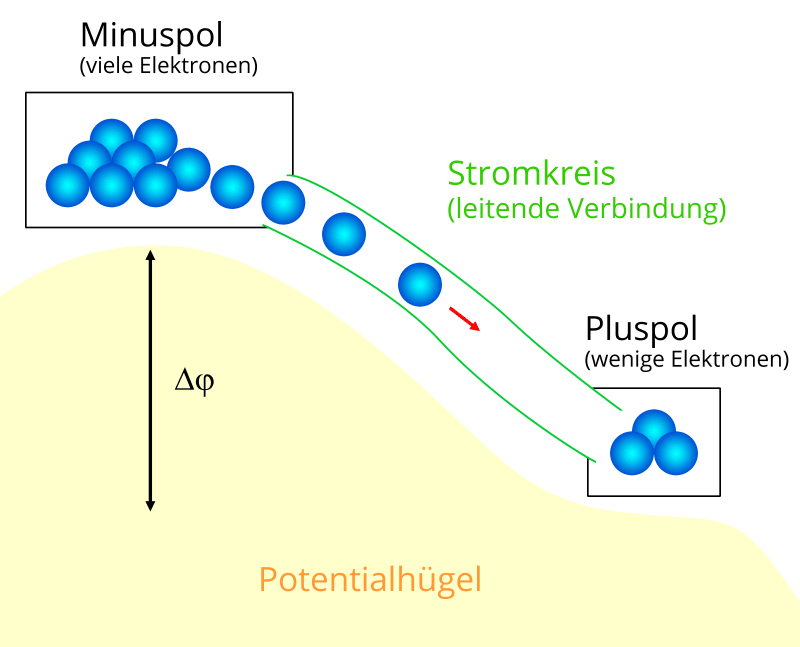
Einige der Elektronen am Minuspol würden eigentlich gerne den Potenzialhügel herunterrollen, um ihre potenzielle Energie zu verringern und einen Ladungsausgleich zwischen Minus- und Pluspol herzustellen.
Das geht aber nur, wenn eine leitende Verbindung zwischen Minus- und Pluspol hergestellt wird, also wenn man einen Stromkreis an die Batterie anschließt. (Mindestens ein elektrisches Bauteil des Stromkreises muss einen elektrischen Widerstand besitzen, sonst gibt es einen Kurzschluss!)
Dann entsteht ein Stromfluss, also ein Fluss von Elektronen vom Minus- zum Pluspol. Dabei verrichtet das elektrische Feld Arbeit und somit nimmt die potenzielle Energie der Elektronen ab.
Die Größe der Spannung kannst du dir als Höhe des Hügels vorstellen. Eine hohe Spannung entspricht einem hohen Hügel. Dann rollen die Elektronen sehr schnell den Hügel hinab und die Stromstärke ist groß. Der Hügel und damit die Spannung ist umso höher, je größer der Unterschied zwischen der Elektronenanzahl am Minus- und am Pluspol ist.
Je mehr Elektronen zum Pluspol rollen, desto kleiner wird der Hügel – die Batterie entlädt sich und die von ihr gelieferte Spannung wird kleiner. Wenn ein Ladungsausgleich eingetreten ist (gleiche Elektronenanzahl an beiden Polen), dann ist der Hügel verschwunden, die Batterie ist jetzt leer und die Potenzialdifferenz bzw. die Spannung ist null.
-
Was ist der Unterschied zwischen Wechselspannung und Gleichspannung?
Die Spannung, die von einer Spannungsquelle geliefert wird, muss nicht unbedingt konstant sein. Man unterscheidet deshalb zwischen Wechselspannung und Gleichspannung:
- Eine Spannung wird Wechselspannung genannt, wenn sich ihre Polarität periodisch mit der Zeit ändert. Das bedeutet, dass ihr Wert immer wieder und in regelmäßigen Abständen das Vorzeichen wechselt. Auch der Betrag der Spannung kann sich ändern. Mit dem Vorzeichen wechselt auch die Fließrichtung des elektrischen Stroms. Aus unseren Steckdosen kommt ein sinusförmiger Wechselstrom, der 50-mal in der Sekunde die Polung ändert.
- Die Polarität einer Gleichspannung bleibt gleich. Hier kann sich zwar der Betrag der Spannung ändern, nicht jedoch das Vorzeichen. Der Strom fließt so immer in die gleiche Richtung. Gleichspannungen werden beispielsweise von Batterien geliefert.
Besonders zu Beginn begegnet dir im Physikunterricht eher die Gleichspannung. Dass aus unseren Steckdosen Wechselspannung kommt, hat technische Gründe. Wenn wir Strom vom Kraftwerk in unsere Wohnungen transportieren wollen, dann treten Verluste auf, unter anderem, weil die Leitungen einen ohmschen Widerstand besitzen. Bei hohen Spannungen sind die Verluste vergleichsweise gering, deshalb nutzen wir Hochspannungsleitungen. Für unsere Geräte brauchen wir aber kleinere Spannungswerte. Mit der Wechselspannung und Transformatoren können wir die Spannung bequem hoch- und runterregeln.
-
Wozu braucht man Spannung?
Wie du jetzt weißt, ist die Spannung die Ursache für den Stromfluss. Wann immer wir also unsere elektrischen Geräte mit Strom betreiben wollen, brauchen wir eine Spannung! Und ohne elektrische Geräte (wie z. B. Handys, Laptops, Küchengeräte, Straßenbahnen, E-Bikes usw.) sähe unser Alltag ganz schön anders aus! Wann immer du ein elektrisches Gerät einschaltest oder verwendest, nutzt du also die elektrische Spannung.
Wenn der Akku deines Handys leer ist, dann kann er auch keine Spannung mehr liefern. Deshalb schaltet sich dein Handy dann ab – denn ohne Spannung auch kein Strom! Wenn du dein Handy dann mit der Steckdose verbindest, lädst du den Akku wieder auf. Dabei werden die Ladungsträger in der Batterie wieder getrennt und dadurch kann die Batterie nach dem Aufladen wieder eine Spannung liefern.