Zwei im Jahr 1845 erstmals von Gustav Robert Kirchhoff aufgestellte Regeln zur Berechnung der Strom- und Spannungsverteilung in elektrischen Stromkreisen.
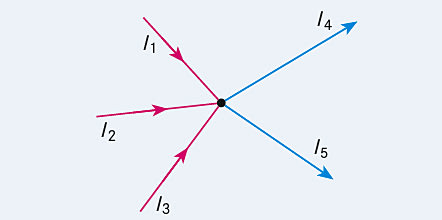
- Knotenregel (1. Kirchhoff’sche Regel): In jedem Verzweigungspunkt (Knoten) in einem Leitersystem ist die Summe der Stromstärken der zufließenden Ströme gleich der Summe der Stromstärken der abfließenden Ströme. Physikalisch steckt dahinter einfach die Ladungserhaltung: Alle an einem Punkt einfließende Ladung muss diesen auch wieder verlassen, da elektrische Ladungen weder zerstört noch erzeugt werden können.
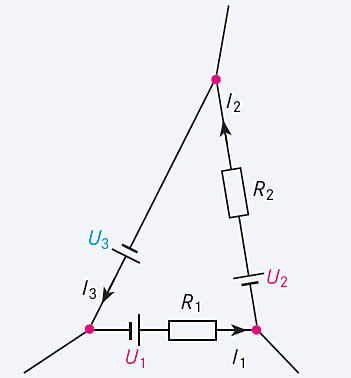
- Maschenregel (2. Kirchhoff’sche Regel): In jedem in sich geschlossenen Teil eines Leitersystems (jeder „Masche“) ist die Summe der Teilspannungen an den Widerständen gleich der Summe der Urspannungen aller in der Masche enthaltenen Stromquellen. Hinter dieser Regel steckt die Energieerhaltung, genauer die Erhaltung der elektrischen Energie – wenn eine Probeladung einmal im Kreis durch ein elektrisches Feld bzw. Potenzial läuft, darf sie dabei keine Energie gewinnen oder verlieren (genauso wenig wie ein Planet, der das Schwerefeld der Sonne umkreist).