-
Aufgabe 1
Eine Familie will ihren Bedarf an Wärmeenergie (thermischer Energie) für Heizung und Warmwasser teilweise durch eine thermische Solaranlage (kurz: Solaranlage) decken. Anhand der Angaben des Solaranlagenherstellers und der Verbrauchswerte der Familie aus dem letzten Kalenderjahr wurde das folgende Modell für ein beispielhaftes Kalenderjahr aufgestellt. Die Leistung der Solaranlage wird durch die Funktion \(f\) mit der Gleichung:
\(f(t)=t^4-24t^3+144t^2+400,\ t\in \mathbb R\)
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion \(g\) mit der Gleichung:
\(g(t)=-t^4+26t^3-167,5t^2-12,5t+2053,\ t\in\mathbb R\)
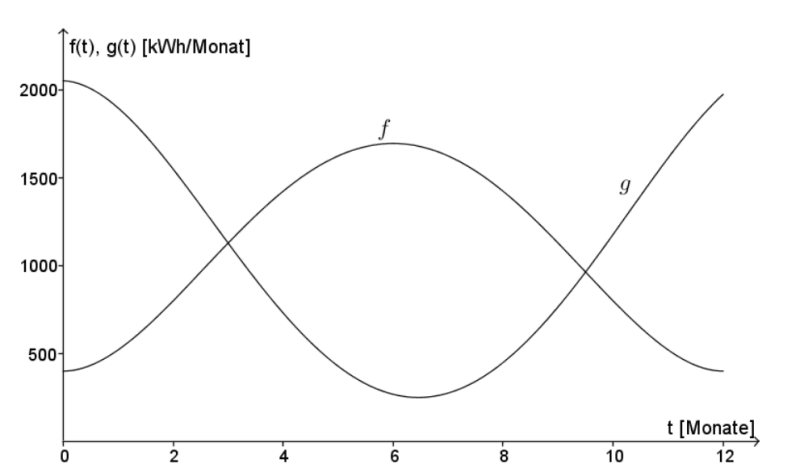
modelliert, und zwar für das Zeitintervall \([0;12]\), das dem Kalenderjahr entspricht. Dabei fasst man \(t\) als Maßzahl zur Einheit 1 Monat und \(f(t)\) sowie \(g(t)\) als Maßzahlen zur Einheit 1 Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat 30 Tage.) Der Zeitpunkt \(t=0\) entspricht dem Beginn des Kalenderjahres. Die Graphen von \(f\) und \(g\) sind in der nachfolgenden Abbildung dargestellt.(1)
Vergleichen Sie die Graphen von f und g im Sachzusammenhang.
(2)
Berechnen Sie \(\frac {f(0)}{g(0)}\) und interpretieren Sie den Wert im Sachzusammenhang.
(3)
Zeigen Sie, dass die Leistung der Solaranlage zu den Zeitpunkten \(t_1=3 \) und
\(t_2=9,5\) dem Leistungsbedarf der Familie entspricht.(5 + 5 + 4 Punkte)
Abiturprüfung
Mathematik
Abitur