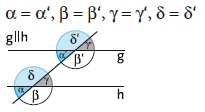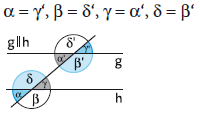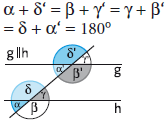Wenn zwei parallele Geraden an einer sog. Doppelkreuzung von einer dritten Geraden geschnitten werden, so gelten für die acht dabei auftretenden Winkel die folgenden Winkelsätze:
- Stufenwinkelsatz
An geschnittenen Parallelen sind die an den beiden Kreuzungen einander entsprechenden Winkel (Stufenwinkel, F-Winkel) gleich groß.
- Wechselwinkelsatz
An geschnittenen Parallelen sind die dem jeweiligen Scheitelwinkel an der anderen Kreuzung entsprechenden Winkel (Wechselwinkel, Z-Winkel) jeweils gleich groß.
- Nachbarwinkelsatz
An geschnittenen Parallelen ergänzen sich die dem jeweiligen Nebenwinkel an der anderen Kreuzung entsprechenden Winkel (Nachbarwinkel, E-Winkel) jeweils zu 180˚.
Die Bezeichnungen F- und Z-Winkel kommen daher, dass man z. B. bei Stufenwinkeln ein schräges „F“ erkennen kann, wenn man den unteren Teil der schrägen Gerade und die rechten Hälften von g und h betrachtet. Bei Wechselwinkeln bilden dann der Mittelabschnitt der schneidenden Gerade sowie die linke Hälfte von g und die rechte von h ein schräges „z“. Beim E-Winkel kann man, wenn man will, ein kleines „e“ (eigentlich eher ein „c“) erkennen.