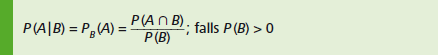Zusammengesetzte Zufallsexperimente
BEISPIELE
- Mehrmaliges Werfen eines Würfels.
- Mehrmaliges Ziehen einer Kugel aus einer Urne mit/ohne Zurücklegen.
Unabhängige Ereignisse: Das Eintreten eines Ereignisses beeinflusst nicht das Eintreten eines anderen Ereignisses.
BEISPIELE
- Mehrmaliges Ziehen einer Kugel aus einer Urne mit Zurücklegen vor jedem erneuten Zug.
- Geburt eines Kindes; Merkmal Geschlecht.
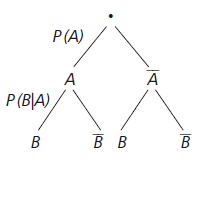
Bedingte Wahrscheinlichkeit von \(A\) unter der Bedingung \(B\):
Wahrscheinlichkeit eines Ereignisses \(A\), das abhängig ist von einem anderen Ereignis \(B\), das mit einer bestimmten Wahrscheinlichkeit \(P (B)\) eingetreten ist.
BEISPIEL
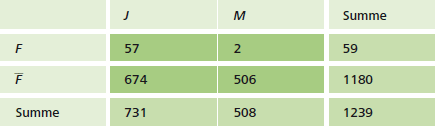
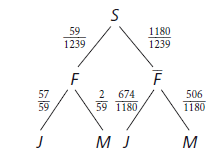
Beim Sehtest in einer Schule werden \(1239\) Jungen \((J)\) und Mädchen \((M)\) auf Rotgrünschwäche (eine Form von „Farbenblindheit“ \(F\)) untersucht. Die folgende Vierfeldertafel dokumentiert das Ergebnis der Untersuchung:
Wir berechnen folgende Wahrscheinlichkeiten für ein zu fällig ausgewähltes Mitglied \(S\) der Schülerschaft :
- \(S\) ist ein Junge, unter der Bedingung \(S\) ist farbenblind:
\(P (J | F) = P_F (J) =\frac{P(J \cap F)}{P (F)} = \frac{57}{1 239} : \frac{59}{1 239} = \frac{57}{59} \approx 0,967\)
Anders gesagt: Falls ein zufällig bestimmtes Mitglied der Schulgemeinschaft farbenblind ist, so ist es mit \(96,7 %\)-iger Wahrscheinlichkeit ein Junge.
- \(S\) ist ein Mädchen, falls \(S\) farbenblind:
\(P (M | F) = P_F (M) = \frac{P(M\cap F)}{P(F)} = \frac{2}{59} \approx 0,034\)
- \(S\) ist farbenblind, falls \(S\) ein Junge ist:
\(P (F | J) = P_J (F) = \frac{P (J\cap F)}{ P(J)} = \frac{57}{731} \approx 0,078\)
- \(S\) ist farbenblind, falls \(S\) ein Mädchen ist:
\(P (F | M) = P_M (F) = \frac{P(M\cap F)}{P(M)} = \frac{2}{508} \approx 0,004\)
- \(S\) ist farbenblind:
\(P (F) = \frac{59}{1 239} \approx 0,048\)
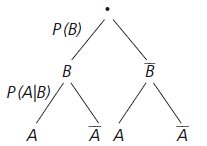
Aus der Definition der bedingten Wahrscheinlichkeit ergibt sich der Multiplikationssatz (hier auch: Pfadregel)
Die bedingte Wahrscheinlichkeit tritt bei mehrstufigen Versuchen auf. Diese lassen sich als Pfade in einem Baumdiagramm darstellen. Jeder Pfad entspricht einem Ereignis des (hier zweistufigen) Zufallsversuchs.
BEISPIEL
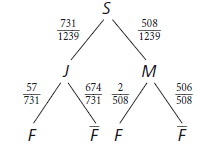
Wahrscheinlichkeit, dass ein zufällig bestimmtes Mitglied der Schulgemeinschaft ein farbenblinder Junge ist
\(P (F \cap J) = \frac{731}{1 239} \cdot \frac{57}{731} \approx 0,046\)
Vertauscht man die Reihenfolge der Stufen in dieser Abbildung, so ändert sich die Wahrscheinlichkeit eines Pfades aufgrund des Multiplikationssatzes nicht.
BEISPIEL
\(P (J \cap F) = \frac{59}{1 239} \cdot \frac{57}{59} \approx 0,046\)
Mehrstufige Zufallsexperimente
Um die Wahrscheinlichkeit eines Ergebnisses bei einem mehrstufigen Zufallsexperiment zu erhalten, notiert man die Wahrscheinlichkeiten der jeweiligen Stufe des Experiments in einem Pfad eines Baumdiagramms (auch Wahrscheinlichkeitsbaum oder Ergebnisbaum) und multipliziert die Einzelwahrscheinlichkeiten (Pfadregel).
(Bei vielen Zufallsexperimenten genügt es, das Baumdiagramm so weit zu skizzieren, dass man das Ergebnis ablesen kann.)
BEISPIEL
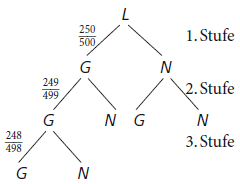
In einer Lostrommel befinden sich noch \(500\) Lose. Die Hälfte davon sind Gewinne, die anderen sind Nieten. Bestimme die Wahrscheinlichkeit, aus dieser Trommel zwei Gewinne (drei Gewinne) hintereinander zu ziehen.
\(P (2 \text{Gewinne}) = \frac{250}{500} \cdot \frac{249}{499} \approx 0,249 \triangleq 24,9 %\)
\(P (3 \text{Gewinne}) = \frac{250}{500} \cdot \frac{249}{499} \cdot \frac{248}{498} \approx 0,124 \triangleq 12,4 %\)
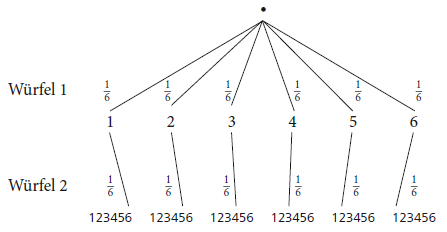
BEISPIEL Zwei Würfel werden geworfen. Wie groß ist die Wahrscheinlichkeit, Augenzahl \(7\) zu würfeln?
\(P (Augenzahl 7) = \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} + \frac{1}{6} \cdot \frac{1}{6} = 6 \cdot \frac{1}{36} = \frac{1}{6}\)
Bernoulli-Experimente
Zufallsexperimente, bei denen zwei Ergebnisse auft reten können (Erfolg/kein Erfolg).
BEISPIEL Ein Spielwürfel wird \(10\)-mal geworfen. Wie groß ist die Wahrscheinlichkeit, dass genau dreimal eine \(6\) gewürfelt wird?
\(p (6) = \frac{1}{6}\) ; \(n = 10\) ; \(k = 3\)
\(P = \begin{pmatrix} 10 \\ 3 \end{pmatrix} \cdot \left(\frac{1}{6}\right)^3 \cdot \left( 1 - \frac{1}{6} \right)^{10 - 3} = \frac{10 \cdot 9 \cdot 8}{1 \cdot 2 \cdot 3} \cdot \frac{1}{6^3} \cdot \frac{5^7}{6^7} \approx 0,155 = 15,5 %\)