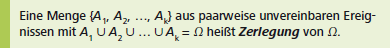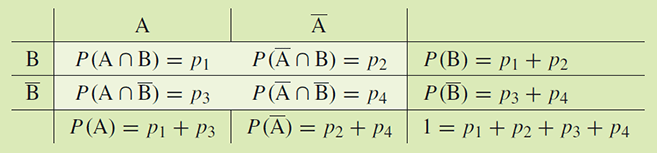Rechengesetze
Für \(A, B, C \in \mathcal P (\Omega )\) gilt:
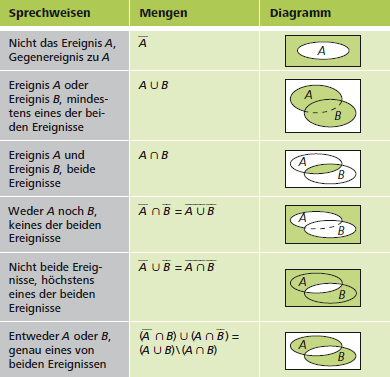
- \(A \cap B = B \cap A; A \cup B = B \cup A;\) Kommutativgesetze
- \((A \cap B) \cap C = A \cap (B \cap C); (A \cup B) \cup C = A \cup (B \cup C);\) Assoziativgesetze
- \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C); A \cup (B \cap C) = (A \cup B) \cap (A \cup C);\) Distributivgesetze
- \(A \cup \big\{ \big\} = A; A \cap \Omega = A;\) Gesetze der neutralen Elemente
- \(A \cap \big\{ \big\} = \big\{ \big\}; A \cup \Omega = \Omega ;\) Gesetze der dominanten Elemente
- \(A \cup \overline{A}= \Omega ; A \cap \overline{A} = \big\{\big\}; \overline{\overline{A}} = A\); Gesetze für das komplementäre Element
- \(A \cup A = A; A \cap A = A;\) Idempotenzgesetze
- \(A \cup (A \cap B) = A; A \cap (A \cup B) = A;\) Absorptionsgesetze
- \(\overline{A \cup B} = \overline{A} \cap \overline{B} ; \overline{A \cap B} = \overline{A} \cup \overline{B}\) Gesetze von de Morgan.
Jedes Ereignis \(A \subseteq \Omega\) lässt sich als Vereinigung von elementaren Ereignissen, d. h. Ergebnissen schreiben: \(A = \bigcup_{\omega \epsilon A}^{} \{\omega \}\).
Beispiel:
Ein Spieler setzt beim Roulette je einen Chip auf „rot“ und auf „gerade“/„Pair“.
\(A =\) „Eine rote Zahl gewinnt.“ \(= \big\{1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36\big\};\)
\(B =\) „Eine gerade Zahl gewinnt.“ \(= \big\{2, 4, 6, ..., 34, 36\big\}.\)
\(C =\) „Keiner der beiden Chips gewinnt.“
\(C = \overline{A} \cap \overline{B}=\overline{A \cup B} = \big\{0, 11, 13, 15, 17, 29, 31, 33, 35\big\}\)
Vierfeldertafel
Beim Berechnen von Wahrscheinlichkeiten ist es oft zweckmäßig, sich die Wahrscheinlichkeiten der einzelnen Ereignisse in einer Vier- oder Mehrfeldertafel zu veranschaulichen. Man bildet dazu eine Zerlegung der Ergebnismenge \(\Omega\) in Ereignisse Ai, die
- (1) jeweils eine positive Wahrscheinlichkeit besitzen: \(P(A_i) > 0\) für alle i,
- (2) paarweise unvereinbar sind: \(A_i \cap A_j = \varnothing\) ; für \(i \neq j\),
- (3) vereinigt das sichere Ereignis ergeben: \(A_1 \cup A_2 ...\cup A_m = \Omega\) .
Sind A und B zwei Ereignisse aus \(\Omega\) , hat die Vierfeldertafel die Form: